Если найти нужную задачу не удаётся, Вы можете оформить Заказ.
Как использовать поиск
| Номер | Условие задачи | Предмет | Задачник | Цена | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3246 |
Плоская световая волна интенсивности I = 0,7 Вт/см2 освещает круглую пластинку с идеально зеркальной поверхностью. Радиус пластинки r=5 см. Найти силу светового давления F, испытываемую пластинкой. |
Физика атома | 50₽ | |||||||||||||||
| 3247 |
На сколько электрон-вольт надо увеличить внутреннюю энергию иона He+, находящегося в основном состоянии, чтобы он мог испустить фотон, соответствующий головной (самой длинноволновой) линии серии Бальмера |
Физика атома | 50₽ | |||||||||||||||
| 3248 |
Релятивистская частица, масса покоя которой m0, движется с кинетической энергией Е. Найти: длину волны де Бройля частицы λ. Расчет провести для электрона с Ек = 1 МэВ. |
Физика атома | 75₽ | |||||||||||||||
| 3249 |
Внутри сферической полости радиуса R = 10 пм находится частица массы т = 1,67∙10-27 кг. Используя соотношение неопределённостей, оценить минимально возможную энергию частицы Emin. |
Физика атома | 50₽ | |||||||||||||||
| 3250 |
Найти среднее расстояние |
Физика атома | 30₽ | |||||||||||||||
| 3251 |
Протон и электрон прошли одинаковую ускоряющую разность потенциалов Δφ = 15 кВ. Во сколько раз отличается коэффициент прозрачности De для электрона и Dp для протона, если высота барьера U = 20 кэВ, а ширина d = 0,1 пм? |
Физика атома | 50₽ | |||||||||||||||
| 3252 |
Период полураспада Т радиоактивного нуклида равен 1 ч. Определить среднюю продолжительность τ жизни этого нуклида. |
Физика атома | 30₽ | |||||||||||||||
| 3254 | Геометрия | 30₽ | ||||||||||||||||
| 3255 |
Написать уравнения плоскостей, параллельных плоскости 2x+2y+z-8=0 и удаленных от нее на расстояние d=4. |
Геометрия | 10₽ | |||||||||||||||
| 3256 |
Стержень, имеющий собственную длину 1 м, направлен в собственной системе отсчета под углом 45° к оси х. Найти длину этого стержня в лабораторной системе отсчета, в которой он движется вдоль оси х' со скоростью v = 0,8∙c. |
Специальная теория относительности | 5.5 | Физика. Чертов, Воробьев | 75₽ | |||||||||||||
| 3257 |
Какова должна быть кинетическая энергия частицы с массой покоя m01, чтобы ее масса была бы такой же, как и масса частицы с массой покоя m02, ускоренной до энергии Eк2? |
Специальная теория относительности | 50₽ | |||||||||||||||
| 3258 |
Найти, при каких действительных $x$ и $y$ справедливо равенство, если $z=x+iy$. |
Теория функций комплексного переменного | 50₽ | |||||||||||||||
| 3259 |
а) записать комплексное число z в показательной форме;
|
Теория функций комплексного переменного | 50₽ | |||||||||||||||
| 3260 |
Дано комплексное число $z=\frac4{1-i \sqrt 3}$. Требуется записать число z в алгебраической и тригонометрической формах. |
Теория функций комплексного переменного | 20₽ | |||||||||||||||
| 3261 |
Представить заданную функцию w=f(z), где z=x+iy в виде $w=2z^2-iz$, $w=u(x,y)+iv(x,y)$, проверить, является ли она аналитической. Если да, то найти значение её производной в заданной точке $z_0=1-i$ |
Теория функций комплексного переменного | 30₽ | |||||||||||||||
| 3262 |
Разложить функцию f(z) в ряд Лорана в окрестности точки $z_0$ и определить область сходимости этого ряда $$f(z)=\frac1{z(z-1)},z_0=0$$ |
Теория функций комплексного переменного | 50₽ | |||||||||||||||
| 3263 |
Вычислить контурный интеграл от функции комплексной переменной с помощью вычетов $$\oint\limits_{C}\frac{e^z}{(4z^2+\pi^2)^2}dz, C:\left| z\right|=\pi$$ |
Теория функций комплексного переменного | 75₽ | |||||||||||||||
| 3264 |
Решить уравнение $x(4+7i)+y(5-3i)=2+6i$ |
Теория функций комплексного переменного | 10₽ | |||||||||||||||
| 3265 |
1) Записать число a в алгебраической форме; |
Теория функций комплексного переменного | 100₽ | |||||||||||||||
| 3266 |
1) Записать число a в алгебраической форме; |
Теория функций комплексного переменного | 75₽ | |||||||||||||||
| 3268 |
Доказать эквивалентность функций $$e^\alpha-1 \sim \alpha$$ |
Введение в анализ | 30₽ | |||||||||||||||
| 3269 |
Задана функция $$f(x)=14^{\frac{1}{6-x}}$$ и два значения аргумента $x_1=4$ и $x_2=6$. Требуется: |
Введение в анализ | 20₽ | |||||||||||||||
| 3270 |
Задана функция |
Введение в анализ | 20₽ | |||||||||||||||
| 3271 |
Построить график функции $y=A\cos(ax+b)$ преобразованием графика функции $y=\cos(x)$ |
Введение в анализ | 30₽ | |||||||||||||||
| 3272 |
Исследовать функции методами дифференциального исчисления и на основании результатов исследования построить их графики. $$y=\frac{8(x-1)}{(x+1)^{2}}$$ |
Введение в анализ | 20₽ | |||||||||||||||
| 3273 |
Исследовать функции методами дифференциального исчисления и на основании результатов исследования построить их графики. $$y=x-\ln(x+1)$$ |
Введение в анализ | 50₽ | |||||||||||||||
| 3274 |
Данная линия называется «Четырёх лепестковая роза».Построить линию в полярной системе координат. |
Введение в анализ | 30₽ | |||||||||||||||
| 3275 |
Нарисовать график гармонического колебания $i(t)=-\cos(2t+\pi/3)$, исходя из графика функции $y=\cos(2t)$, где I-амплитуда тока, ω-угловая частота гармонических колебаний, t-текущее время, θ –начальная фаза тока. Указать амплитуду, период и угловую частоту колебания. |
Введение в анализ | 30₽ | |||||||||||||||
| 3276 |
В задаче задана функция $y=f(x)$. Исследовать данную функцию на непрерывность и построить ее график. |
Введение в анализ | 30₽ | |||||||||||||||
| 3277 |
Задана функция |
Введение в анализ | 10₽ | |||||||||||||||
| 3278 |
Найти область определения функции $$f(x)=\frac{1}{x^2-x-12}$$ |
Введение в анализ | 15₽ | |||||||||||||||
| 3279 |
Исходя из определения производной, найти производную функции $f(x)=3\sin x + \cos x$ |
Введение в анализ | 20₽ | |||||||||||||||
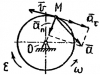
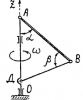
| 3281 |
|
Теоретическая механика | C2.7_1 | Теоретическая механика | 300₽ | |||||||||||||
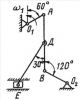
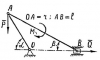
| 3282 |
В точке А заменить подвижный шарнир на НЕ ПОДВИЖНЫЙ. |
Теоретическая механика | C3.7_1 | Теоретическая механика | 300₽ | |||||||||||||
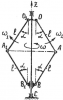
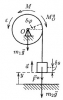
| 3283 | Теоретическая механика | C4.7_1 | Теоретическая механика | 300₽ | ||||||||||||||
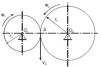
| 3284 |
КИНЕМАТИКА ТОЧКИ
|
Теоретическая механика | K1.7_1 | Теоретическая механика | 300₽ | |||||||||||||
| 3285 |
|
Теоретическая механика | K4.7 | Теоретическая механика 2 | 300₽ | |||||||||||||
| 3286 |
|
Теоретическая механика | K5.7 | Теоретическая механика 2 | 300₽ | |||||||||||||
| 3287 |
|
Теоретическая механика | K7.7 | Теоретическая механика 2 | 300₽ | |||||||||||||
| 3289 | Теоретическая механика | Д3.7 | Теоретическая механика 2 | 300₽ | ||||||||||||||
| 3290 |
|
Теоретическая механика | Д6.7 | Теоретическая механика 2 | 300₽ | |||||||||||||
| 3291 | Теоретическая механика | Д8.7 | Теоретическая механика 2 | 200₽ | ||||||||||||||
| 3292 | Теоретическая механика | D5.7 | Теоретическая механика | 300₽ | ||||||||||||||
| 3295 |
Вычислить приближенное значение определенного интеграла: $$\int\limits_{-2}^8 \sqrt{x^3+8} \,dx$$ |
Определенный интеграл | 30₽ | |||||||||||||||
| 3296 |
Вычислить несобственный интеграл или доказать его расходимость: $$\int\limits_2^\infty \frac{\ln x}{x}\,dx$$ |
Несобственный интеграл | 30₽ | |||||||||||||||
| 3297 |
Вычислить длину дуги кривой $r=1 - \cos \varphi (0\le \varphi \le 2\pi) $ |
Определенный интеграл | 50₽ | |||||||||||||||
| 3298 |
Вычислить приближенное значение определенного интеграла $$\int_{1}^{11}\sqrt{x^3+3}dx$$ с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака. |
Определенный интеграл | 50₽ | |||||||||||||||
| 3299 |
Вычислить несобственный интеграл или доказать его расходимость $$\int_{2}^{+\infty}\frac{dx}{x\ln{x}}$$ |
Несобственный интеграл | 30₽ | |||||||||||||||
| 3300 |
Вычислить объём тела, образованного вращением вокруг оси Oy фигуры, ограниченной кривыми $$y=\frac{2}{1+x^2}; y=x^2$$ |
Определенный интеграл | 30₽ | |||||||||||||||
| 3302 |
Вычислить интеграл: $$\int_{0}^{\frac{\pi}{4}}x(\sin{x}-\cos{x})dx$$ |
Определенный интеграл | 30₽ |