Если найти нужную задачу не удаётся, Вы можете оформить Заказ.
Как использовать поиск
| Номер | Условие задачи | Предмет | Задачник | Цена | ||
|---|---|---|---|---|---|---|
| 3355 |
Ток в проводнике изменяется по закону I(t) = 0,2∙t (A). За промежуток времени от t1 = 0 до t2 = 2 с в проводнике выделилось количества тепла Q = 400 Дж. Определить: сопротивление проводника; напряженность электрического поля в момент времени τ = 3 с. Длина проводника l = 2 м. |
Постоянный ток | 50₽ | |||
| 3356 |
ЭДС источника E1 = 10 В. К источнику присоединена катушка из никелинового провода ρ = 4∙10-5 Ом∙см длиной 10 м. КПД такой цепи η = 80%. Определить: скорость упорядоченного движения электронов, считая концентрацию электронов в проводе n = 2,5∙1022 см-3, количество тепла, которое выделяется в 1 см провода за 1 мин. |
Постоянный ток | 50₽ | |||
| 3357 |
При напряжении на концах медного провода U = 17 В плотность тока равна j = 20 А/см2. Найти: 1) напряженность поля в проводе, 2) длину провода. |
Постоянный ток | 30₽ | |||
| 3358 |
Сила тока в проводнике сопротивлением 12 Ом равномерно убывает от 5 А до 0 в течение 10 с. Какое количество теплоты выделяется в этом проводнике за указанный промежуток времени? |
Постоянный ток | 30₽ | |||
| 3359 | Постоянный ток | 30₽ | ||||
| 3360 |
Сколько элементов нужно соединить параллель нов батарею, чтобы при подключении к ней сопротивления 49 Ом получить силу тока в цепи 2 А? ЭДС каждого элемента 100 В. внутреннее сопротивление 2 Ом. |
Постоянный ток | 10₽ | |||
| 3361 |
Электронагреватель, включенный в сеть напряжением 220 В, имеет КПД η и позволяет за время t нагреть воду массой М на Δt, доведя ее до кипения, а часть этой воды массой m обратить в пар. Нагреватель изготовлен из проволок с удельным сопротивлением ρ, длиной L и диаметром d. Определите величину, указанную в таблице знаком вопроса. |
Постоянный ток | 50₽ | |||
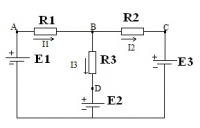
| 3362 |
|
Постоянный ток | 35₽ | |||
| 3363 |
К автомобильному аккумулятору подключены параллельно 2 фары мощностью по 60 Вт. Найти ток разряда аккумулятора, если напряжение на его клеммах 12 В. |
Постоянный ток | 10₽ | |||
| 3364 |
Сила тока в проводнике меняется со временем по закону $I=I_0\sin \omega t$. Найти заряд $q$, протекающий через поперечное сечение проводника за половину периода $Т$, если амплитудное значение силы тока $I_0=10 А$, циклическая частота $\omega=50\pi c^{-1}$. |
Постоянный ток | 30₽ | |||
| 3365 |
Определить сечение медных проводов, отводящих ток от генератора мощностью 103 кВт, если ток передается на трансформатор под напряжением 15 кВ. Плотность тока в проводе не должна превышать 10 А/мм2. |
Постоянный ток | 20₽ | |||
| 3366 |
Из куска провода сопротивлением R = 100 Ом сделано кольцо. В каких точках следует соединить провода, подводящие ток, чтобы сопротивление между ними стало r = 9 Ом? |
Постоянный ток | 10₽ | |||
| 3368 |
Какую максимальную полезную мощность можно получить, имея в своем распоряжении источник с ЭДС E = 45 В и внутренним сопротивлением r = 10 Ом и два нагревателя с сопротивлениями R1 = 5 Ом и R2 = 20 Ом соответственно? |
Постоянный ток | 10₽ | |||
| 3369 |
ЭДС батареи Ɛ = 24 В. Наибольшая сила тока, которую может дать батарея, Imax = 5 А. Какая наибольшая мощность Рmax может выделиться на подключенном к батарее резисторе с переменным сопротивлением R? Чему равен при этом КПД? |
Постоянный ток | 30₽ | |||
| 3370 |
Трансформатор, понижающий напряжение с 220 B до 12 В, содержит в первичной обмотке N1 = 2000 витков. Сопротивление вторичной обмотки R2 = 0,15 Ом. Пренебрегая сопротивлением первичной обмотки, определить число витков во вторичной обмотке, если во внешнюю цепь (в сети пониженного напряжения) передают мощность P=20Вт. |
Постоянный ток | 20₽ | |||
| 3371 |
Определите сопротивление мотка медной проволоки сечением 0,1 мм2, масса мотка 0,3 кг. |
Постоянный ток | 50₽ | |||
| 3372 |
Какая разность потенциалов получается на зажимах двух элементов, включенных параллельно, если их ЭДС E1 = 1,4 В и E2 = 1,2 В и внутренние сопротивления r1 = 0,6 Ом и r2 = 0,4 Ом? |
Постоянный ток | 50₽ | |||
| 3373 |
При замыкании аккумуляторной батареи на резистор сопротивлением 9 Ом в цепи идет ток силой 1 А. Сила тока короткого замыкания равна 10 А. Какую наибольшую полезную мощность может дать батарея? |
Постоянный ток | 30₽ | |||
| 3374 |
Сила тока в проводнике сопротивления R = 100 Ом равномерно нарастает от I0 = 0 до Imax = 10 А в течение времени t = 30 с. Определить количество теплоты Q, выделившееся за это время в проводнике. |
Постоянный ток | 50₽ | |||
| 3408 |
При подключении к аккумулятору с внутренним сопротивлением r=2 Ом нагревательный элемент развивает мощность N1 = 50 Вт. При подключении нагревательного элемента к двум таким аккумуляторам, соединенным последовательно, выделяемая в нагревателе мощность составила N2 = 72 Вт. Найти сопротивление R нагревателя. |
Постоянный ток | 10₽ | |||
| 3409 |
Вычислить неопределенный интеграл: $$\int{\frac{x^4-x^3-9x^2-10x-14}{x^2-2x-8}}dx$$ |
Неопределённый интеграл | 30₽ | |||
| 3410 |
Даны векторы $\vec{а}(а_1; а_2; а_3), \vec{b}(b_1; b_2; b_3), \vec{с}(с_1; с_2; с_3)$ и $\vec{d}(d_1; d_2; d_3)$ в некотором базисе. Показать, что векторы $\vec{а}, \vec{b}, \vec{с}$ образуют базис и найти координаты вектора $\vec{d}$ в этом базисе. |
Аналитическая геометрия | 50₽ | |||
| 3411 |
Дана система линейных уравнений. Доказать ее совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления. |
Алгебра | 50₽ | |||
| 3412 |
Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее $x''_1, x''_2, x''_3$ через $x_1, x_2, x_3$. |
Алгебра | 50₽ | |||
| 3413 |
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей: $$A_\varphi=\left(\begin{array}{ccc} |
Алгебра | 30₽ | |||
| 3414 |
Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка $4x^2+24xy+11y^2=20$. |
Алгебра | 30₽ | |||
| 3415 |
Экспериментально получены пять значений искомой функции y=f(x) при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию y=f(x) в виде y=a∙x+b. |
Алгебра | 50₽ | |||
| 3416 |
Дана система линейных уравнений. Доказать ее совместность и решить тремя способами: 1) методом Крамера; 2) методом Гаусса; 3) средствами матричного исчисления. |
Алгебра | 50₽ | |||
| 3417 |
Решить систему линейных уравнений по правилу Крамера |
Алгебра | 30₽ | |||
| 3418 |
Решить систему линейных уравнений по правилу Гаусса: $$\left\{ |
Алгебра | 30₽ | |||
| 3419 |
Решить систему линейных уравнений матричным методом: $$\left\{ |
Алгебра | 30₽ | |||
| 3420 |
При каких значениях p и q область значений функции $y=4\sqrt{x-p}+3\sqrt{q-x}$ совпадает с её областью определения? |
Алгебра | 50₽ | |||
| 3421 |
Решить систему линейных уравнений методом Крамера $$\left\{ |
Алгебра | 30₽ | |||
| 3422 |
Решить систему линейных уравнений методом Гаусса $$\left\{ |
Алгебра | 50₽ | |||
| 3423 |
Вычислить определитель $$\begin{vmatrix} |
Алгебра | 50₽ | |||
| 3424 |
Найти обратную матрицу $$A=\begin{pmatrix} |
Алгебра | 30₽ | |||
| 3425 |
Найти собственные числа и собственные векторы матрицы $$A=\begin{pmatrix} |
Алгебра | 50₽ | |||
| 3426 |
В задаче, используя метод Гаусса, найти решение системы или доказать ее несовместимость. $$\left\{ |
Алгебра | 30₽ | |||
| 3427 |
В задаче дана матрица $$A=\begin{pmatrix} |
Алгебра | 50₽ | |||
| 3428 |
Найти $x_3$ по формулам Крамера. |
Алгебра | 50₽ | |||
| 3429 |
Решить систему уравнений методом Гаусса |
Алгебра | 10₽ | |||
| 3430 |
Решить систему уравнений методом Гаусса |
Алгебра | 20₽ | |||
| 3431 |
Решить систему уравнений методом Гаусса |
Алгебра | 20₽ | |||
| 3432 |
Решить систему уравнений |
Алгебра | 5₽ | |||
| 3433 |
Решить систему уравнений |
Алгебра | 20₽ | |||
| 3434 |
Решить систему уравнений |
Алгебра | 10₽ | |||
| 3435 |
Решить систему уравнений |
Алгебра | 5₽ | |||
| 3436 |
Решить систему уравнений |
Алгебра | 5₽ | |||
| 3437 |
Пересекаются ли в одной точке прямые |
Алгебра | 5₽ | |||
| 3438 |
Решить систему уравнений методом Крамера и с помощью обратной матрицы $$\left\{ |
Алгебра | 30₽ |