Если найти нужную задачу не удаётся, Вы можете оформить Заказ.
Как использовать поиск
| Номер | Условие задачи | Предмет | Задачник | Цена | ||
|---|---|---|---|---|---|---|
| 3691 |
Построить прямые линии, заданные параметрами 1) b=-2, φ=60°;2) b=-2, φ=120°.Написать их уравнения |
Аналитическая геометрия | 10₽ | |||
| 3692 |
На числовой оси построить точки A(1), В(-3) и C(-2) и найти величины АВ, BC, и СА отрезков на оси. Проверить, что АВ + BC + СА = 0. |
Аналитическая геометрия | 10₽ | |||
| 3693 |
На плоскости построить точки $A(-7;0)$ и $B(0;1)$ и точки $А_1$ и $В_1$, симметричные с $A$ и $B$ относительно биссектрисы первого и третьего координатных углов. Вычислить периметр трапеции $А В В_1 А_1$. |
Аналитическая геометрия | 30₽ | |||
| 3694 |
На оси ординат найти точку, одинаково удаленную от начала координат и от точки A(-2;5). |
Аналитическая геометрия | 10₽ | |||
| 3695 |
На оси абсцисс найти точку, удаленную от точки $A(-2;3)$ на $3\sqrt 5$ единиц. |
Аналитическая геометрия | 10₽ | |||
| 3696 |
Определить центр и радиус круга, описанного около треугольника с вершинами A(-3;-1), B(5;3) и C(6;-4). |
Аналитическая геометрия | 20₽ | |||
| 3697 |
Написать уравнение плоскости, проходящей через точку A(2;-1;1) и перпендикулярной к плоскостям 3x+2y-z+4=0 и x+y+z-3=0. Построить ее. |
Аналитическая геометрия | 20₽ | |||
| 3698 |
Написать уравнение плоскости, проходящей через точки M(0;-5;0) и N(0;0;2) и перпендикулярной к плоскости x+5y+2z-10=0. Построить ее. |
Аналитическая геометрия | 20₽ | |||
| 3699 |
Написать уравнение плоскости, проходящей через ось Ox и составляющей угол 60° с плоскостью y = x. |
Аналитическая геометрия | 30₽ | |||
| 3700 |
Даны декартовы прямоугольные координаты вершин пирамиды $А_1 А_2 А_3 А_4$. |
Аналитическая геометрия | 100₽ | |||
| 3701 |
Заданы плоскость π и точка М. |
Аналитическая геометрия | 50₽ | |||
| 3702 |
Написать уравнение плоскости τ, проходящей через точки $М_1(-4;5;-4)$ и $М_2(-1;-4;-4)$ перпендикулярно заданной плоскости $\pi: |
Аналитическая геометрия | 30₽ | |||
| 3703 |
Даны прямая l и точка М. |
Аналитическая геометрия | 100₽ | |||
| 3704 |
Даны уравнения прямых $l_1 и l_2$: |
Аналитическая геометрия | 50₽ | |||
| 3705 |
В ромб с диагоналями d1 = 36 и d2 = 18 вписан эллипс так, что больший из диаметров эллипса лежит на большей из диагоналей ромба. Сторона ромба в точке касания с эллипсом делится в отношении n:m = 5:4. Вычислить: |
Аналитическая геометрия | 150₽ | |||
| 3706 |
Дано: $\vec a=2\vec i + \vec j + \vec k;$ $\vec b = \{-2;1;1\}; A(3,0,1); B(0,1,-2)$. |
Аналитическая геометрия | 75₽ | |||
| 3707 |
Найти: |
Аналитическая геометрия | 50₽ | |||
| 3708 |
Найти площадь треугольника с вершинами в точках A(7,3,4), B(1,0,6), C(4,5,-2). Решить средствами векторной алгебры. |
Аналитическая геометрия | 20₽ | |||
| 3709 |
Даны точки A(3;3;-2), B(0;-3;4), C(0;-3;0), D(0;2;-4). Найти векторы (AB) = a и (CD) = b и найти проекцию вектора b на направление вектора a. |
Аналитическая геометрия | 30₽ | |||
| 3710 |
Через ось Oz проведена плоскость, составляющая с плоскостью $2x+y-\sqrt{5}z=0$, угол 60°. Найти уравнение этой плоскости. Решить методами аналитической геометрии. |
Аналитическая геометрия | 20₽ | |||
| 3711 |
Найти точку пересечения прямой $$\frac x2=\frac{y-1}{1}=\frac{z+1}{2}$$ с плоскостью $x-2y+3z-29=0$. |
Аналитическая геометрия | 20₽ | |||
| 3712 |
Найти координаты точек пересечения кривых. Указать вид кривых. Сделать рисунок. |
Аналитическая геометрия | 10₽ | |||
| 3713 |
Составить уравнение и построить линию, расстояние каждой точки которой от точки A(2;0) и от прямой 5x+8=0 относятся как 5:4. |
Аналитическая геометрия | 30₽ | |||
| 3714 |
Даны координаты вершин пирамиды $А_1 А_2 А_3 А_4$. Найти: |
Аналитическая геометрия | 100₽ | |||
| 3715 |
Найти координаты вершин треугольника, если даны координаты одной его вершины B(7;15) и уравнения его биссектрисы: 4x+7y-23=0 и медианы 2x-y-1=0, проведенных из одной вершины. |
Аналитическая геометрия | 50₽ | |||
| 3716 |
Привести к простейшему виду уравнения линии второго порядка, определить её тип и сделать схематический рисунок. Все вычисления проводить с точностью до 0,01. |
Аналитическая геометрия | 50₽ | |||
| 3717 |
Установить, какая линия определяется данным уравнением. Изобразить линию на чертеже. |
Аналитическая геометрия | 30₽ | |||
| 3718 |
Установить, какая линия определяется данным уравнением. Изобразить линию на чертеже. |
Аналитическая геометрия | 30₽ | |||
| 3719 |
Даны координаты вершин пирамиды $А_1(7, 7, 6), А_2(5, 10, 6), А_3(5, 7, 12), А_4(7, 10, 4)$. Найти: |
Аналитическая геометрия | 75₽ | |||
| 3720 |
Установить, какие линии определяются данными уравнениями. Изобразить линии на чертеже. $y^2-16x-6y+25=0$ |
Аналитическая геометрия | 30₽ | |||
| 3721 |
Установить, какие линии определяются данными уравнениями. Изобразить линии на чертеже. $y=-3-\sqrt{21-4x-x^2}$ |
Аналитическая геометрия | 30₽ | |||
| 3722 |
Дано уравнение $y=f(x)$ кривой, точка $x_0$ и уравнение прямой $Ax+By+C=0$. Требуется: |
Аналитическая геометрия | 50₽ | |||
| 3723 |
Установить, какие линии определяются данными уравнениями. Изобразить линии на чертеже. $4x^2+3y^2-8x+12y-32=0$ |
Аналитическая геометрия | 30₽ | |||
| 3724 |
Установить, какие линии определяются данными уравнениями. Изобразить линии на чертеже. $x=2-\sqrt{6-4y}$. |
Аналитическая геометрия | 30₽ | |||
| 3725 |
Дано уравнение $y=f(x)$ кривой, точка $x_0$ и уравнение прямой $Ax+By+C=0$. Требуется: |
Аналитическая геометрия | 75₽ | |||
| 3726 |
Даны координаты вершин пирамиды $А_1(7, 7, 6), А_2(5, 10, 6), А_3(5, 7, 12), А_4(7, 10, 4)$. Найти: |
Аналитическая геометрия | 75₽ | |||
| 3727 |
Установить, какие линии определяются данными уравнениями. Изобразить линии на чертеже. $y^2-16x-6y+25=0$. |
Аналитическая геометрия | 30₽ | |||
| 3729 |
Составьте уравнение плоскости, проходящей через точку $А (2; 2; 2)$ и отсекающей равные отрезки на осях координат. |
Аналитическая геометрия | 30₽ | |||
| 3730 |
Составить каноническое уравнение эллипса, проходящего через точки $M(\frac{\sqrt{5}}{2};\frac{\sqrt{5}}{5});N(-2;\frac{\sqrt{15}}{5})$. |
Аналитическая геометрия | 30₽ | |||
| 3731 |
Угол между асимптотами гиперболы равен α=60° градусов. Вычислить эксцентриситет гиперболы |
Аналитическая геометрия | 30₽ | |||
| 3732 |
Даны вершины треугольника A(4;13), B(-1;1), C(7;7). |
Аналитическая геометрия | 75₽ | |||
| 3733 |
Даны вершины треугольника A(-1;-1), B(5;2), C(2;3). |
Аналитическая геометрия | 75₽ | |||
| 3734 | Электромагнетизм | 50₽ | ||||
| 3735 |
Протон прошел ускоряющую разность потенциалов U и стал двигаться в однородном магнитном поле (B = 0,5 Тл) по винтовой линии с шагом h = 5 см и радиусом R = 0,5 см. Определить ускоряющую разность потенциалов, которую прошел протон. |
Электромагнетизм | 20₽ | |||
| 3736 | Электромагнетизм | 30₽ | ||||
| 3737 |
Кольцо из медного провода массой m = 20 г помещено в однородное магнитное поле (B = 0,5 Тл) так, что плоскость кольца составляет угол α = 20° с линиями магнитной индукции. Определить заряд Q, который пройдет по кольцу, если снять магнитное поле. |
Электромагнетизм | 30₽ | |||
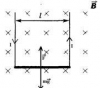
| 3738 |
Протон с кинетической энергией Т = 1 МэВ влетел в однородное магнитное поле перпендикулярно линиям индукции (В = 1 Тл). Какова должна быть минимальной протяженность поля в направлении, по которому первоначально летел протон, чтобы направление его движения изменилось на противоположное? |
Электромагнетизм | 30₽ | |||
| 3739 |
|
Электромагнетизм | 50₽ | |||
| 3740 |
|
Электромагнетизм | 100₽ | |||
| 3741 | Электромагнетизм | 75₽ |