Если найти нужную задачу не удаётся, Вы можете оформить Заказ.
Как использовать поиск
| Номер | Условие задачи | Предмет | Задачник | Цена | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16893 |
Зная постоянную Авогадро NA, определить массу mA нейтрального атома углерода 12C и массу m, соответствующую углеродной единице массы. |
Физика атома | 30₽ | |||||||||
| 16894 |
Хлор представляет собой смесь двух изотопов с относительными атомными массами Ar1=34,969 и Ar2=36,966. Вычислить относительную атомную массу Ar, хлора, если весовые доли ω1 и ω2 первого и второго изотопов соответственно равны 0,754 и 0,246. |
Физика атома | 30₽ | |||||||||
| 16895 |
Бор представляет собой смесь двух изотопов с относительными атомными массами Ar1=10,013 и Ar2=11,009. Определить массовые доли ω1 и ω2 первого и второго изотопов в естественном боре. Относительная атомная масса Ar бора ровна 10,811. |
Физика атома | 30₽ | |||||||||
| 16896 |
Ядро радия ${_{88}^{226}}Ra$ выбросило $\alpha$ - частицу (ядро атома гелия ${_2^4}He$. Найти массовое число $A$ и зарядовое число $Z$ вновь образовавшегося ядра. По таблице Д. И. Менделеева определить, какому элементу это ядро соответствует. |
Физика атома | 30₽ | |||||||||
| 16897 |
Ядро азота ${_7^{14}}N$ захватило $\alpha$-частицу и испустило протон. Определить массовое число $A$ и зарядовое число $Z$ образовавшегося в результате этого процесса ядра. Укачать, какому элементу это ядро соответствует. |
Физика атома | 30₽ | |||||||||
| 16898 |
На столе лежит лист бумаги. Луч света, падающий на бумагу под углом ε = 30°, даст на ней светлое пятно. Насколько сместится это пятно, если на бумагу положить плоскопараллельную стеклянную пластину толщиной d = 5 см? |
Оптика | 30₽ | |||||||||
| 16899 |
Луч падает под углом ε = 60° на стеклянную пластинку толщиной d = 30 мм. Определить боковое смещение ∆x луча после выхода из пластинки. |
Оптика | 30₽ | |||||||||
| 16900 |
Луч света переходит из среды с показателем преломления n1 в среду с показателем преломления п2. Показать, что если угол между отраженным и преломленным лучами равен π/2, то выполняется условие tg ε1 = n2/n1 (ε1 — угол падения). |
Оптика | 30₽ | |||||||||
| 16901 |
Луч света падает на грань призмы с показателем преломления n под малым углом. Показать, что если преломляющий угол Θ призмы мал, то угол отклонения α лучей не зависит от угла падения и равен Θ(n - 1). |
Оптика | 30₽ | |||||||||
| 16902 |
Из стекла требуется изготовить плосковыпуклую линзу, оптическая сила Ф которой равна 5 дптр. Определить радиус R кривизны выпуклой поверхности линзы. |
Оптика | 30₽ | |||||||||
| 16903 |
Найти grad z и производную в точке A(0;3) по направлению вектора a=(1;-2), если $$z=\ln(5x^2+4y^2)$$ |
Векторный анализ | 50₽ | |||||||||
| 16904 |
Найти область определения функции $$z=\sqrt{1-\frac{x^2}{9}+\frac{y^2}{16}}$$ |
МАТЕМАТИКА | 20₽ | |||||||||
| 16905 |
Задано движение точки координатным способом и некоторый момент времени. Найти траекторию точки. Для заданного момента времени найти положение точки, скорость, ускорение, касательное и нормальное ускорение, радиус кривизны траектории. Все найденные величины изобразить на рисунке в подходящем масштабе так, чтобы все векторы были хорошо видны.
|
Теоретическая механика | 300₽ | |||||||||
| 16906 |
Выполнить указанные действия: $$z=(3-2i)^2+\frac{9-8i}{4+2i}-i^5$$ |
Теория функций комплексного переменного | 30₽ | |||||||||
| 16907 |
Найти действительные решения уравнения: $$(1+3i)x+(2-i)^2 y=(-1-4i)i$$ |
Теория функций комплексного переменного | 30₽ | |||||||||
| 16908 |
Дать геометрическое описание множества точек комплексной плоскости, удовлетворяющих указанному условию $$\renewcommand{\Re}{\mathop{\mathrm{Re}}\nolimits}\Re(zi)>3$$ |
Теория функций комплексного переменного | 30₽ | |||||||||
| 16909 |
Представить комплексные числа $z_1$ и $z_2$ в тригонометрической и экспоненциальной формах и изобразить точками на комплексной плоскости $$z_1=-3-3\sqrt{3}i, z_2=-2i$$ |
Теория функций комплексного переменного | 50₽ | |||||||||
| 16910 |
Для комплексных чисел $z_1$ и $z_2$, записанных в тригонометрической форме, выполнить указанные действия $$z_1\cdot z_2, \frac{z_1^3}{z_2}, \sqrt[5]{z_2}$$ $$z_1=6\left(\cos\left(-\frac{2}{3}\pi\right)+i\sin\left(-\frac{2}{3}\pi\right)\right)$$ $$z_2=2\left(\cos\left(-\frac{\pi}{2}\right)+i\sin\left(-\frac{\pi}{2}\right)\right)$$ |
Теория функций комплексного переменного | 75₽ | |||||||||
| 16911 |
Найти корни многочлена второй степени (с комплексными коэффициентами) на множестве комплексных чисел и разложить его на множители. $$Q(x)=x^2-7x+2ix+9-7i$$ |
Теория функций комплексного переменного | 50₽ | |||||||||
| 16912 |
Составить многочлен с действительными коэффициентами третьей степени, если $x_1=-0.5$ и $x_2=6-i$ – два из его корней. |
Теория функций комплексного переменного | 50₽ | |||||||||
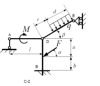
| 16913 | Теоретическая механика | 400₽ | ||||||||||
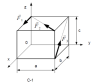
| 16914 | Теоретическая механика | 250₽ | ||||||||||
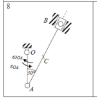
| 16915 |
|
Теоретическая механика | 500₽ | |||||||||
| 16916 |
Дать геометрическое описание множества точек комплексной плоскости, удовлетворяющих указанному условию $$\frac{\pi}{2}\le \frac{\pi}{2}+\arg z \le \pi$$ |
Теория функций комплексного переменного | 30₽ | |||||||||
| 16917 |
Найти корни многочлена второй степени (с комплексными коэффициентами) на множестве комплексных чисел и разложить его на множители: $$Q(x)=x^2+2x+2ix-4+2i$$ |
Теория функций комплексного переменного | 30₽ | |||||||||
| 16918 |
Составить многочлен с действительными коэффициентами четвёртой степени, если $x_1=-2$ – корень многочлена кратности 2 и $x_2=4i$ – один из других корней многочлена. |
Теория функций комплексного переменного | 30₽ | |||||||||
| 16919 |
Докажите, что многочлен $x^3-19x^2+9x-2$ не имеет отрицательных корней. |
Алгебра | 50₽ | |||||||||
| 16920 |
Вычислить $\frac{\partial z}{\partial x}$ и $\frac{\partial z}{\partial y}$, если $$z=(\cos{ xy})\cdot \ln(x^2+y)+\frac{1}{4} \arccos{\sqrt{1-xy}}$$ |
Дифференциальное исчисление функций нескольких переменных | 30₽ | |||||||||
| 16921 |
Вычислить производные $\frac{\partial u}{\partial t}$ и $\frac{\partial u}{\partial s}$ сложной функции $$u=2\tan\frac{z}{x-y}+x^3 y^4 z^2,$$ если $$x=3\cos s, y=3+t^2s^2, z=\ln\sqrt{1+t^2}$$ |
Дифференциальное исчисление функций нескольких переменных | 30₽ | |||||||||
| 16922 |
Найти все производные второго порядка для функции $$u=\sin(xy+z)+x^6y^7z^8$$ |
Дифференциальное исчисление функций нескольких переменных | 30₽ | |||||||||
| 16923 |
Вычислить $du$ и $d^2u$ для функции $$u=x^4 y^5+\cos(xy)$$ |
Дифференциальное исчисление функций нескольких переменных | 30₽ | |||||||||
| 16924 |
Вычислить $у'$ для функции $у(x)$, заданной неявно: $$y=\ln(\sqrt{x}-\sqrt{y})$$ |
Дифференциальное исчисление функций нескольких переменных | 30₽ | |||||||||
| 16925 |
Найти частные производные $\frac{\partial z}{\partial x}$ и $\frac{\partial z}{\partial y}$ для функции $z(x,y)$, заданной неявно: $$x+y+z=e^z$$ |
Дифференциальное исчисление функций нескольких переменных | 30₽ | |||||||||
| 16926 |
Написать уравнение касательной плоскости и нормали к поверхности, заданной уравнением $$z=y\tan\frac{x}{a}$$ в точке $M_0 \left(\frac{\pi a}{4},a,a\right)$. |
Дифференциальное исчисление функций нескольких переменных | 50₽ | |||||||||
| 16927 |
Исследовать на экстремум функцию $$z=xy+\frac{50}{x}+\frac{20}{y}$$ при $х>0, у>0$. |
Дифференциальное исчисление функций нескольких переменных | 50₽ | |||||||||
| 16928 |
Найти наибольшее и наименьшее значения функции $z=x^2+y^2$ в области $$x^2+y^2\le 100$$ |
Дифференциальное исчисление функций нескольких переменных | 50₽ | |||||||||
| 16930 |
Найти массу пластины, ограниченной линиями $$L_1: x^2+y^2=a^2; L_2: x^2+y^2=ax; L_3:x=0,(y≥0),$$ |
Кратные и криволинейные интегралы | 75₽ | |||||||||
| 16931 |
Найти объем тела, ограниченного поверхностями $$S_1: x^2+y^2+z^2=a^2; S_2: x^2+y^2\le z^2; S_3: z=0, (z\ge 0)$$ |
Кратные и криволинейные интегралы | 150₽ | |||||||||
| 16932 |
Найти центр тяжести однородного тела, ограниченного указанными поверхностями: $$S_1:z=\sqrt{x^2+y^2}; S_2: z=2$$ |
Кратные и криволинейные интегралы | 150₽ | |||||||||
| 16933 |
Вычислить массу контура прямоугольника $ABCD$, если линейная плотность в каждой его точке определяется выражением $$\delta=yz$$ $$A(0,0,0),B(0,4,0),C(0,4,2),D(0,0,2)$$ |
Кратные и криволинейные интегралы | 100₽ | |||||||||
| 16934 |
Найти координаты центра тяжести части однородной поверхности конуса $$z=\sqrt{x^2+y^2},$$ вырезанной цилиндром $$x^2+y^2=2x$$ |
Кратные и криволинейные интегралы | 150₽ | |||||||||
| 16935 |
Найти производную скалярного поля $$U(x,y,z)=x^3 y-xy^3+6z$$ в точке $M\left(2;-\frac12;1\right)$ по направлению нормали к поверхности $$S: z^2=x^2+4y^2-4,$$ образующей острый угол с положительным направлением оси $OZ$. |
Векторный анализ | 150₽ | |||||||||
| 16936 |
Найти работу векторного поля $$\vec{a}=x\vec{i}+y\vec{j}+(x+y-1)\vec{k}$$ при перемещении точки вдоль линии $L$ от точки $М$ к точке $N$, где $L$ - ломаная, соединяющая точки $M(1,1,1),K(2,3,1),N(2,3,4)$. |
Векторный анализ | 100₽ | |||||||||
| 16937 |
Найти поток векторного поля $$\vec{a}=z^2\vec{i}+xz\vec{j}+y^2\vec{k}$$ через часть поверхности $$S:x^2+y^2=4-z,$$ вырезанную плоскостью $P:z=0$, непосредственно и с помощью формулы Гаусса-Остроградского (нормаль внешняя к замкнутой поверхности). |
Векторный анализ | 100₽ | |||||||||
| 16938 |
Найти циркуляцию вектора $$\vec{a}=-y\vec{i}+x\vec{j}-zx\vec{k}$$ по контуру $$Г:\left\{\begin{array}{ll} |
Векторный анализ | 100₽ | |||||||||
| 16939 |
Проверить потенциальность поля вектора $$\vec{a}=x\vec{i}-\frac{y\vec{j}+z\vec{k}}{y^2+z^2},$$ найти потенциал. |
Векторный анализ | 150₽ | |||||||||
| 16941 |
Найти общее решение дифференциального уравнения $$y''+12y'+9y=x\sin x+\cos x$$ |
Дифференциальные уравнения | 75₽ | |||||||||
| 16942 |
Найти общее решение дифференциального уравнения $$y'''+3y''+2y'=3x^2+2x$$ |
Дифференциальные уравнения | 50₽ | |||||||||
| 16943 |
Найти общее решение дифференциального уравнения $$y''-9y=e^{-3x}\sin 3x$$ |
Дифференциальные уравнения | 50₽ | |||||||||
| 16944 |
Найти общее решение дифференциального уравнения $$y''+34y'+289y=e^{-17x}$$ |
Дифференциальные уравнения | 50₽ |