Если найти нужную задачу не удаётся, Вы можете оформить Заказ.
Как использовать поиск
| Номер | Условие задачи | Предмет | Задачник | Цена | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16689 |
ЛАБОРАТОРНАЯ РАБОТА «ФОТОЭФФЕКТ» |
Фотоэффект | 750₽ | |||||||||||||||||||||
| 16690 | МАТЕМАТИКА | 200₽ | ||||||||||||||||||||||
| 16691 |
Петя, Вася и Толя на уроке физкультуры по очереди бросают друг другу волейбольный мяч. Первым его бросает Петя. Найдите число способов, которыми мяч может вернуться обратно к Пете через 23 броска (не обязательно впервые). |
МАТЕМАТИКА | 200₽ | |||||||||||||||||||||
| 16692 |
Вычислить $$\iint\limits_\sigma (3x^2+5y^2+3z^2-2) d\sigma,$$ где $\sigma$ – часть поверхности $y=\sqrt{x^2+z^2}$, отсечённая плоскостями $y=0, y=1$. Изобразить график. |
Кратные и криволинейные интегралы | 100₽ | |||||||||||||||||||||
| 16693 |
Между двумя скрещенными поляроидами помещена пластинка в полволны. Оптическая ось пластинки параллельна оси одного из поляроидов, на систему падает пучок естественного света интенсивностью, равной Iест (в единицах СИ). Чему равна интенсивность света, прошедшего через систему? |
Оптика | 150₽ | |||||||||||||||||||||
| 16695 |
В длинный вертикальный цилиндрический сосуд наливают воду, температура которой t0 = 0 °C. Высота уровня воды в сосуде H = 20 м. На сколько изменится высота содержимого сосуда, если температура воды внутри сосуда понизится до t1 = -0,01 °C? Удельная теплота плавления льда q = 335 кДж/кг, плотность льда ρл = 920 кг/м3. Изменение температуры ΔТ плавления льда можно считать связанным с изменением внешнего давления Δр соотношением |
Молекулярная физика и термодинамика | 200₽ | |||||||||||||||||||||
| 16696 |
|
Молекулярная физика и термодинамика | 200₽ | |||||||||||||||||||||
| 16697 |
|
Молекулярная физика и термодинамика | 300₽ | |||||||||||||||||||||
| 16698 |
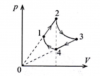
Один моль гелия находится при температуре T = 273 К Далее газ расширяется так, что объём и давление увеличиваются на 2 %. Изменения параметров газа считать малыми.
|
Молекулярная физика и термодинамика | 200₽ | |||||||||||||||||||||
| 16699 |
Медианы AA1, BB1, CC1 треугольника ABC пересекаются в точке M, причём AC = 12, BM = 4. Найдите AA12 + BB12 + CC12. |
Геометрия | 150₽ | |||||||||||||||||||||
| 16700 |
Точки P, Q, R лежат соответственно на сторонах AB, BC, AC треугольника ABC, причём AP:PB = 2:5, BQ:QC = 1:4, а площадь треугольника PQR составляет 31/70 площади треугольника ABC. Найдите AR:RC. |
Геометрия | 200₽ | |||||||||||||||||||||
| 16701 |
Точки K и L лежат на боковых сторонах AB и CD трапеции ABCD соответственно, причём площадь четырёхугольника BCLK в 5 раз меньше площади четырёхугольника ADLK; CL = 3, DL = 15, CK = 4, KL⊥AB. Найдите DK. |
Геометрия | 200₽ | |||||||||||||||||||||
| 16702 |
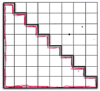
В таблице 10x10 половина клеток красные, половина – синие. Назовём строку и столбец чистыми, если в них все клетки одного цвета. Какое наибольшее суммарное число чистых строк и столбцов может быть в такой таблице и почему? |
МАТЕМАТИКА | 150₽ | |||||||||||||||||||||
| 16703 | Геометрия | 300₽ | ||||||||||||||||||||||
| 16704 |
|
Молекулярная физика и термодинамика | 300₽ | |||||||||||||||||||||
| 16705 | Геометрия | 300₽ | ||||||||||||||||||||||
| 16706 |
Выполнить действия с комплексными числами $z_1=\alpha_1+i\beta_1,z_2=\alpha_2+i\beta_2,z_3=\alpha_3+i\beta_3$ в алгебраической форме. $$\alpha_1=-3, \beta_1=-4, \alpha_2=6, \beta_2=8, \alpha_3=6, \beta_3=1$$Вычислить: $$1) (z_1+i)(1-z_2); 2) \frac{\bar{z_2}}{z_3}$$ |
Теория функций комплексного переменного | 30₽ | |||||||||||||||||||||
| 16707 |
Выполнить действия с комплексными числами $z_1=\alpha_1+i\beta_1,z_2=\alpha_2+i\beta_2,z_3=\alpha_3+i\beta_3$ в тригонометрической форме. $$\alpha_1=-3, \beta_1=-\sqrt{3}, \alpha_2=6, \beta_2=-6, \alpha_3=6, \beta_3=6$$ Вычислить: $$1) z_1\cdot z_2; 2) \frac{z_1}{\bar{z_3}}; 3) {z_1}^5; 4) \sqrt[3]{z_1}$$ |
Теория функций комплексного переменного | 100₽ | |||||||||||||||||||||
| 16708 |
Выяснить, какие области удовлетворяют условию $\alpha$: |
Теория функций комплексного переменного | 30₽ | |||||||||||||||||||||
| 16709 |
Заданы множества |
Теория множеств | 30₽ | |||||||||||||||||||||
| 16710 |
Для данной формулы $\alpha$ алгебры логики записать таблицу истинности. $$\alpha=\left[(\bar{A}\vee \bar{C}) \& \bar{B}\right] \vee \left[ (\bar{A} \to B) \sim C\right]$$ |
Математическая логика | 30₽ | |||||||||||||||||||||
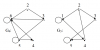
| 16711 | Теория графов | 30₽ | ||||||||||||||||||||||
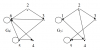
| 16712 | Теория графов | 30₽ | ||||||||||||||||||||||
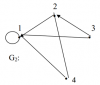
| 16713 | Теория графов | 50₽ | ||||||||||||||||||||||
| 16714 |
Две лампочки соединены в электрической цепи параллельно. Вероятность того, что первая лампочка выйдет из строя равна p1, а вероятность неисправности второй лампочки равна p2. Найти вероятность того, что: |
Теория вероятностей | 30₽ | |||||||||||||||||||||
| 16715 |
В урне находится k белых, M красных и r черных шаров. Наудачу вынимаются n шаров. Найти вероятность того, что из них окажется: k = 8; M = 6; r = 5; n = 3 |
Теория вероятностей | 50₽ | |||||||||||||||||||||
| 16716 |
В ящике находится k деталей, принадлежащих цеху № 1, M деталей – цеху № 2 и r деталей – цеху № 3. Вероятность того, что деталь окажется бракованной для цеха № 1, равна p1, для цеха № 2 – p2, а цех № 3 производит n % брака. Наудачу ОТК отбирает на проверку деталь, найти вероятность того, она окажется стандартной. |
Теория вероятностей | 50₽ | |||||||||||||||||||||
| 16717 |
Выполнены многократные измерения длины объекта. Требуется построить доверительный интервал с надежностью для оценки математического ожидания количественного признака X – неизвестной длины объекта. Данные измерений приведены в таблице по вариантам.
|
Математическая статистика | 50₽ | |||||||||||||||||||||
| 16718 |
Для выборки объема n, определить среднее выборочное, выборочную дисперсию, «исправленную» выборочную дисперсию. Построить таблицу, содержащую интервальный вариационный ряд. Построить гистограмму, график эмпирической функции распределения, если выборка задана по вариантам. |
Математическая статистика | 200₽ | |||||||||||||||||||||
| 16719 |
Какой максимальный объем крови может протекать через артерию с внутренним диаметром 4 мм, чтобы течение было ламинарным? Коэффициент вязкости крови 5 мПа·с. Критическое значение числа Рейнольдса для гладких цилиндрических труб 2300. Плотность крови 3050 кг/м3. При какой максимальной скорости крови течение в артерии стало бы турбулентным? Достижима ли такая скорость? |
Биофизика | 030 | ИжГСХА. Физика с основами биофизики. 2013 год | 50₽ | |||||||||||||||||||
| 16720 |
Определить толщину стенки локтевой кости, если ее разрыв произошел при осевой нагрузке 1295 Н. Внешний диаметр кости в месте разрыва 13 мм, предел прочности на разрыв 16,2 МПа. |
Биофизика | 031 | ИжГСХА. Физика с основами биофизики. 2013 год | 50₽ | |||||||||||||||||||
| 16721 |
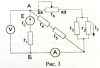
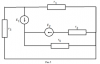
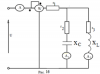
|
Электротехника | 250₽ | |||||||||||||||||||||
| 16722 | Электротехника | 250₽ | ||||||||||||||||||||||
| 16723 |
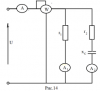
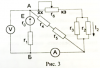
|
Электротехника | 300₽ | |||||||||||||||||||||
| 16724 |
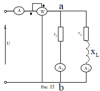
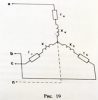
|
Электротехника | 300₽ | |||||||||||||||||||||
| 16725 |
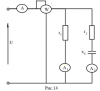
|
Электротехника | 300₽ | |||||||||||||||||||||
| 16726 |
|
Электротехника | 400₽ | |||||||||||||||||||||
| 16727 | Электротехника | 250₽ | ||||||||||||||||||||||
| 16728 |
|
Электротехника | 250₽ | |||||||||||||||||||||
| 16729 |
|
Электротехника | 400₽ | |||||||||||||||||||||
| 16730 |
Длина большеберцовой кости у лежащей собаки равна 36 см, площадь поперечного сечения ее в среднем равна 85 мм2. Определить уменьшение длины кости у собаки, когда она стоит, если масса собаки 24 кг. Модуль Юнга 4,5·1010 Па. |
Биофизика | 032 | ИжГСХА. Физика с основами биофизики. 2013 год | 50₽ | |||||||||||||||||||
| 16731 |
Сухожилие длиной 75 мм и площадью поперечного сечения 80 мм2 при нагрузке 9,5 Н удлиняется на 15 мм. Определить модуль упругости для этого сухожилия и вычислить для него объемную плотность энергии. |
Биофизика | 033 | ИжГСХА. Физика с основами биофизики. 2013 год | 50₽ | |||||||||||||||||||
| 16732 |
Вычислить величину упругого напряжения, возникающего при подвешивании к портняжной мышце лягушки грузика массой 10 г. Площадь сечения мышцы 2,7 мм2. Какова будет работа, необходимая для растяжения мышцы под действием веса грузика, если ее длина возросла от 25 мм до 34 мм? Модуль упругости мышцы при этом растяжении равен 0,95 МПа. |
Биофизика | 034 | ИжГСХА. Физика с основами биофизики. 2013 год | 50₽ | |||||||||||||||||||
| 16733 |
Нормальная длина портняжной мышцы лягушки 25 мм. При растяжении до 32 мм модуль упругости мышцы равен 220 кПа, а при растяжении до 36 мм модуль упругости возрастает до 1,58 МПа. Во сколько раз объемная плотность энергии растяжения мышцы во втором случае больше, чем в первом? |
Биофизика | 035 | ИжГСХА. Физика с основами биофизики. 2013 год | 50₽ | |||||||||||||||||||
| 16734 |
При взятии крови на анализ на коже делают надрез, к которому подводят кончик капиллярной трубки. Определить коэффициент поверхностного натяжения крови, если диаметр капилляра 0,3 мм и кровь поднялась в нем на высоту 76 мм. Считать смачивание стенки капилляра полным. Плотность крови 1060 кг/м3. |
Биофизика | 037 | ИжГСХА. Физика с основами биофизики. 2013 год | 30₽ | |||||||||||||||||||
| 16735 |
Для измерения КПН жидкости сравнительным методом используют сталагмометр, представляющий собой трубку малого диаметра, из которой каплями вытекает жидкость фиксированного объема. Определить КПН мочи, если при вытекании одного и того же объема дистиллированной воды и мочи образуется соответственно 150 и 158 капель. Плотности воды и мочи соответственно 1000 и 1020 кг/м3. КПН дистиллированной воды 72,7 мН/м. |
Биофизика | 038 | ИжГСХА. Физика с основами биофизики. 2013 год | 50₽ | |||||||||||||||||||
| 16736 |
Врач прописал больному принимать по 50 капель лекарства. Сколько капель лекарства придется принимать больному, если температура жидкости понизилась и КПН при этом возрастает от 71,9 до 74,3 мН/м? Изменением плотности жидкости пренебречь. |
Биофизика | 039 | ИжГСХА. Физика с основами биофизики. 2013 год | 50₽ | |||||||||||||||||||
| 16737 |
Масса 100 капель физиологического раствора, вытекающего из капилляра, равна 2,21 г. Определить КПН физиологического раствора, если диаметр шейки капли в момент отрыва равен 1 мм. |
Биофизика | 040 | ИжГСХА. Физика с основами биофизики. 2013 год | 50₽ | |||||||||||||||||||
| 16738 |
На железнодорожной платформе у начала второго вагона покоящегося поезда стоял пассажир. Поезд тронулся с места и далее двигался равноускоренно. При этом оказалось, что третий вагон поезда проезжал мимо пассажира в течение времени τ. В течение какого времени будет проезжать мимо пассажира пятый вагон? Вагоны поезда пронумерованы по порядку с начала поезда и имеют одинаковую длину. Пассажир неподвижен. |
Кинематика | 150₽ | |||||||||||||||||||||
| 16739 |
Тело, брошенное со скоростью v0 = 10 м/с под углом α = 45° к горизонту, дважды проходит высоту h = 2 м. На каком расстоянии находятся точки прохождения этой высоты? |
Кинематика | 100₽ |