Если найти нужную задачу не удаётся, Вы можете оформить Заказ.
Как использовать поиск
| Номер | Условие задачи | Предмет | Задачник | Цена | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16841 |
Положительно заряженный шарик (q = 1,5·10–6 Кл) массой m = 10 г является частью математического маятника. Маятник поместили в однородное электрическое поле, силовые линии которого направлены вертикально вверх. Величина напряженности поля E = 2·104 В/м. Определите во сколько раз изменится период гармонических колебаний шарика, если направление напряженности электрического поля изменится на противоположное. |
Электродинамика | 100₽ | |||||||||||||||||||
| 16842 | Теоретическая механика | 300₽ | ||||||||||||||||||||
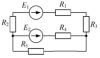
| 16843 |
|
Электротехника | 100₽ | |||||||||||||||||||
| 16844 | Теоретическая механика | C1.1 | Теоретическая механика 2 | 300₽ | ||||||||||||||||||
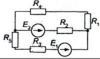
| 16845 |
|
Электротехника | 250₽ | |||||||||||||||||||
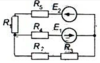
| 16846 |
|
Электротехника | 150₽ | |||||||||||||||||||
| 16848 |
Есть четыре различные пентамино (пятиклеточные фигурки). Известно, что как ни разбивай их на пары, пентамино в каждой паре можно сложить так, что получатся две одинаковые фигуры. Приведите пример, как такое может быть. |
МАТЕМАТИКА | 200₽ | |||||||||||||||||||
| 16849 |
Исследовать сходимость несобственного интеграла для подынтегральной функции $$\int_1^{+\infty} \frac{(x+3)dx}{x^5+3x+1}$$ |
Несобственный интеграл | 30₽ | |||||||||||||||||||
| 16850 |
Все рёбра правильной пирамиды SABCD с вершиной S равны 2. Плоскость, параллельная прямым AC и SB, пересекает рёбра AB и BC в точках M и N. Найдите периметр сечения пирамиды этой плоскостью, если $MN=\sqrt{2}$. |
Стереометрия | 200₽ | |||||||||||||||||||
| 16851 |
Вычислить точное значение интеграла $$\int_a^b f(x) dx; a=-0.2, b=0.8, f(x)=(x+0.2)\cdot \sqrt{5x+5}$$ |
Определенный интеграл | 50₽ | |||||||||||||||||||
| 16852 |
Вычислить площадь фигуры, ограниченной графиками данных функциональных зависимостей. Сделать рисунок: $$y=\arccos x, y=0, x=0$$ |
Определенный интеграл | 30₽ | |||||||||||||||||||
| 16853 |
Исследовать сходимость несобственного интеграла для подынтегральной функции $$\int_1^{+\infty}\frac{dx}{\sqrt[3]{x^4}+5x+1}$$ |
Несобственный интеграл | 30₽ | |||||||||||||||||||
| 16854 |
Частица массы m столкнулась с покоившейся частицей массы M и отклонилась на угол π/2, а частица массы M отскочила под углом α (tg α = 0,71) к первоначальному направлению движения частицы массы m. На сколько процентов уменьшилась кинетическая энергия системы в результате столкновения, если отношение масс M/m = 4? |
Механика | 50₽ | |||||||||||||||||||
| 16855 |
Свет нормально падает на плоскопараллельную стеклянную пластинку толщиной 10 мм. Коэффициент преломления стекла равен 1,66, а коэффициент поглощения равен 1,5 м-1. Найти во сколько раз уменьшение интенсивности прошедшего света только за счет отражения превосходит уменьшение интенсивности света только за счет поглощения. Многократные отражения не учитывать. |
Оптика | 75₽ | |||||||||||||||||||
| 16856 |
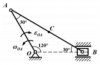
Заряженная частица, ускоренная разностью потенциалов U, влетает в однородное магнитное поле под углом α к направлению поля и начинает двигаться по винтовой линии. Индукция магнитного поля - В. радиус витка винтовой линии - R, шаг винтовой линии - h. Найти неизвестные величины.
|
Электромагнетизм | 100₽ | |||||||||||||||||||
| 16857 |
Для материальной точки массой m написать уравнение синусоидальных колебаний, происходящих с периодом 0,8 с и начальной фазой π/2. Найти массу материальной точки, если максимальная сила, действующая на неё равна 12 мН, а полная энергия колебаний составляет 120 мкДж |
Кинематика | 150₽ | |||||||||||||||||||
| 16858 |
На дифракционную решётку нормально падает монохроматический свет с длиной волны λ = 600 нм. Определите наибольший порядок спектра, полученный с помощью этой решётки и угол дифракции, соответствующей последнему максимуму, если её постоянная d = 2 мкм. |
Оптика | 50₽ | |||||||||||||||||||
| 16859 |
Два одинаковых проводящих заряженных шара находятся на расстоянии r = 30 см. Сила притяжения F1 шаров равна 90 мкН. После того, как шары были приведены в соприкосновение и удалены друг от друга на прежнее расстояние, они стали отталкиваться с силой F2 = 160 мкН. Определить заряды Q1 и Q2, которые были на шарах до их соприкосновения. Диаметр шаров считать много меньшим расстояния между ними. |
Электростатика | 13.9 | Физика. Чертов, Воробьев | 30₽ | |||||||||||||||||
| 16860 |
Электрон в невозбуждённом атоме водорода движется вокруг ядра по окружности радиусом r = 53 пм. Вычислить силу эквивалентного кругового тока I и напряжённость H поля в центре окружности. |
Электромагнетизм | 23.33 | Физика. Чертов, Воробьев | 30₽ | |||||||||||||||||
| 16861 | Постоянный ток | 30₽ | ||||||||||||||||||||
| 16862 |
Напряжение U на шинах электростанции равно 6,6 кВ. Потребитель находится на расстоянии l = 10 км. Определить площадь S сечения медного провода, который следует взять для устройства двухпроводной линии передачи, если сила тока I в линии равна 20 А и потери напряжения в проводах не должны превышать 3%. |
Постоянный ток | 19.3 | Физика. Чертов, Воробьев | 30₽ | |||||||||||||||||
| 16863 |
Найти магнитный поток Ф, создаваемый соленоидом сечением S = 10 см2, если он имеет п = 10 витков на каждый сантиметр его длины при силе тока I = 20 А. |
Электромагнетизм | 24.5 | Физика. Чертов, Воробьев | 30₽ | |||||||||||||||||
| 16864 |
Вычислить объём тела, образованного вращением фигуры, ограниченной графиками функций вокруг оси OX, сделать чертёж: $$y=4x^3;x=0;y=4$$ |
Определенный интеграл | 50₽ | |||||||||||||||||||
| 16865 |
Дано скалярное поле $u=u(x; y)$:
|
Дифференциальное исчисление функций нескольких переменных | 100₽ | |||||||||||||||||||
| 16866 |
Вычислить несобственный интеграл или установить его расходимость: $$\int_0^1 \frac{x^4}{\sqrt{1-x^5}}dx$$ |
Несобственный интеграл | 50₽ | |||||||||||||||||||
| 16867 |
Решить задачу Коши: $$e^x (1+e^y )+y' e^y (1+e^x )=0, y(0)=0$$ |
Дифференциальные уравнения | 30₽ | |||||||||||||||||||
| 16868 |
Решить задачу Коши: $$y'+\frac{1-2x}{x^2}y=1, y(1)=1$$ |
Дифференциальные уравнения | 50₽ | |||||||||||||||||||
| 16869 |
Вычислить приближённо число $A$, предварительно представив его в форме: $$A=f(x+∆x,y+∆y)≈f(x,y)+f_x' (x,y)∆x+f_y' (x,y)∆y$$ для конкретной функции $f(x,y)$ и для любых $x,y,∆x,∆y$. Затем в полученную формулу подставить удобные для расчёта числовые значения $x,y,∆x,∆y$. $$A=\sin \frac{11\pi}{30}\tan\frac{13\pi}{40}$$ |
Дифференциальное исчисление функций нескольких переменных | 30₽ | |||||||||||||||||||
| 16870 |
Данную функциональную зависимость $z=f(x,y)$ исследовать на экстремум: $$z=4x^2-2xy+y^2-2x-4y+1$$ |
Дифференциальное исчисление функций нескольких переменных | 50₽ | |||||||||||||||||||
| 16871 |
Найти общий интеграл дифференциального уравнения |
Дифференциальные уравнения | 50₽ | |||||||||||||||||||
| 16872 |
Найти решение задачи Коши $$y'+y \tanx=\cos^2x,y\left(\frac{\pi}{4}\right)=\frac12$$ |
Дифференциальные уравнения | 50₽ | |||||||||||||||||||
| 16873 |
Найти общий интеграл дифференциального уравнения $$\left(2x-1-\frac{y}{x^2}\right)dx-\left(2y-\frac1x\right)dy=0$$ |
Дифференциальные уравнения | 50₽ | |||||||||||||||||||
| 16874 |
Найти общее решение дифференциального уравнения $$xy'''+y''=x+1$$ |
Дифференциальные уравнения | 50₽ | |||||||||||||||||||
| 16875 |
Найти решение задачи Коши $$y''+2\sin y \cos^3 y=0, y(0)=0, y'(0)=1$$ |
Дифференциальные уравнения | 50₽ | |||||||||||||||||||
| 16876 |
Найти общее решение дифференциального уравнения $$y'''-3y''+3y'-y=2x$$ |
Дифференциальные уравнения | 50₽ | |||||||||||||||||||
| 16877 |
Найти общее решение дифференциального уравнения $$y'''-2y''+y'=(2x+5)e^{2x}$$ |
Дифференциальные уравнения | 50₽ | |||||||||||||||||||
| 16878 |
Найти общее решение дифференциального уравнения $$y''+y=2\cos {7x}+3\sin{7x}$$ |
Дифференциальные уравнения | 50₽ | |||||||||||||||||||
| 16879 |
Найти общее решение дифференциального уравнения $$y''-3y'=2\cosh {3x}$$ |
Дифференциальные уравнения | 50₽ | |||||||||||||||||||
| 16880 |
Найти общее решение дифференциального уравнения $$y''-6y'+8y=\frac{4}{1+e^{-2x}}$$ |
Дифференциальные уравнения | 50₽ | |||||||||||||||||||
| 16881 |
Решить систему дифференциальных уравнений методом Эйлера и операционным методом: |
Дифференциальные уравнения | 100₽ | |||||||||||||||||||
| 16882 |
Исследовать ряд на сходимость: $$\sum_{n=1}^{\infty}\frac{\arcsin \frac{1}{\sqrt{n^2+4}}}{\sqrt{n+\sqrt{n+\sqrt{n}}}}$$ |
Ряды | 30₽ | |||||||||||||||||||
| 16883 |
Исследовать ряд на сходимость: $$\sum_{n=1}^{\infty} \frac{n+2}{2^n\cdot n!}$$ |
Ряды | 50₽ | |||||||||||||||||||
| 16884 |
Исследовать ряд на сходимость: $$\sum_{n=2}^{\infty} \frac{1}{(n+3)\ln^2(2n+1)}$$ |
Ряды | 50₽ | |||||||||||||||||||
| 16885 |
Исследовать ряд на абсолютную и условную сходимость: $$\sum_{n=1}^{\infty} (-1)^{n+1}\frac{2n+1}{n(n+1)}$$ |
Ряды | 50₽ | |||||||||||||||||||
| 16886 |
Вычислить приближенно сумму ряда с заданной точностью ε. Указать N- наименьшее число членов ряда, которое обеспечивает заданную точность суммы ряда: $$\sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n!}; ε=10^{-3}$$ |
Ряды | 50₽ | |||||||||||||||||||
| 16887 |
Найти интервал сходимости степенного ряда. Исследовать поведение ряда на границах интервала: $$\sum_{n=1}^{\infty} \frac{\sqrt[3]{n+2}}{n+1}x^n$$ |
Ряды | 50₽ | |||||||||||||||||||
| 16888 |
Найти интервал сходимости степенного ряда. Исследовать поведение ряда на границах интервала: $$\sum_{n=2}^{\infty} \frac{(x-1)^{n-1}}{3^{n}\ln n}$$ |
Ряды | 50₽ | |||||||||||||||||||
| 16889 |
Разложить функцию f(х) в ряд Тейлора в окрестности точки x0. Найти интервал сходимости разложения. $$f(x)=\frac{1}{\sqrt{x}},x_0=2$$ |
Ряды | 75₽ | |||||||||||||||||||
| 16890 |
Вычислить приближенно с заданной точностью ε значение функции, используя соответствующее разложение функции в степенной ряд. Указать N - наименьшее число членов ряда, обеспечивающее заданную точность: $$\cos{10°}, ε=10^{-4}$$ |
Ряды | 50₽ | |||||||||||||||||||
| 16891 |
Вычислить приближенное точностью ε значение интеграла, разлагая подынтегральную функцию в степенной ряд: $$\int\limits_{0}^{0,5} \frac {1-\cos x}{x^2} \,dx, ε=0,001$$ |
Ряды | 50₽ |