Если найти нужную задачу не удаётся, Вы можете оформить Заказ.
Как использовать поиск
| Номер | Условие задачи | Предмет | Задачник | Цена | ||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 18123 |
Гладкая упругая шайба радиуса R упруго сталкивается с такой же шайбой, покоящейся на гладкой горизонтальной поверхности. В рeзультате столкновения скорость налетающей шайбы уменьшается вдвое. Найдите расстояние d от центра покоящейся шайбы до прямой. по которой двигалась налетающая шайба. Шайбы однородные. |
Механика | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18124 |
Оцените во сколько раз среднее расстояние между молекулами газа при н. у. (р = 105 Па, T = 273 K) больше размера (диаметра) самих молекул. Оцените также отношение объёма газа к суммарному объёму молекул в этом объёме. Диаметр молекул принять равным d=3∙10-10 м. |
Молекулярная физика и термодинамика | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18125 | Электромагнетизм | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 18126 |
На гладкой горизонтальной поверхности в круге радиуса R = 5 м, ограниченном шероховатой вертикальной стенкой, находится брусок. Если бруску сообщить начальную скорость v0 = 4 м/с . направленную по касательной к стенке, то через время Т = 5 с с скорость бруска уменьшается вдвое. Найдите коэффициент μ трения скольжения бруска по поверхности стенки. |
Механика | 30₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18127 |
Горизонтально расположенное тонкое однородное кольцо радиуса R = 0,25 м, сделанное из свинцовой проволоки, вращается вокруг вертикальной оси. проходящей через центр кольца. При какой угловой скорости ω такое кольцо может разорваться, если для свинца предел прочности на разрыв, т. с. максимальная сила в расчёте на единицу площади поперечного сечения $σ = \frac{f}{S}=15\cdot 10^6$ Па? |
Механика | 30₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18128 |
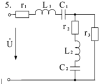
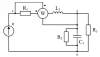
|
Электротехника | 200₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18129 |
У поверхности Земли концентрация молекул азота в 2,6 раз меньше концентрации кислорода. На какой (в км) высоте концентрации этих газов станут равными? Среднюю температуру атмосферы считать равной 280 К. |
Молекулярная физика и термодинамика | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18130 | Электростатика | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 18131 |
Пусть $x_1=a>1$ и $x_{n+1}=\frac{x_n+1}{2}$ при $n\ge 1$. Используя теорему о пределе монотонной последовательности, докажите, что $$\lim\limits_{n\to\infty} x_n=1$$ |
Пределы | 100₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18132 |
В одной школе обучалось вдвое больше девочек, чем мальчиков. Директор школы ввёл обычай: ежедневно поутру каждый мальчик должен был делать поклон директору, каждому из своих товарищей мальчиков и каждой девочке. Каждая девочка также должна была делать поклон директору, каждой своей подруге и каждому мальчику. Этот церемонный обычай строго соблюдался и поэтому ежедневно утром можно было насчитать 900 поклонов. Сколько в школе было мальчиков и сколько было девочек? |
Комбинаторика | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18133 |
Разложить на множители: $$(b-c)^3+(c-a)^3+(a-b)^3$$ |
Алгебра | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18134 |
Сравнить два числа: $$\sqrt{10+\sqrt{24}+\sqrt{40}+\sqrt{60}}\ и\ 5,3$$ |
Алгебра | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18135 |
Решить в целых числах уравнение: $$x^2+2x=y^4+y^2$$ |
Алгебра | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18136 |
Решить неравенство: $$\frac{|x-1|-|x|}{|2x-3|-|x+1|}\le 0$$ |
Алгебра | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18137 |
Решить уравнение:$$\sin^3x-\sin x\cos 2x-2\sin x-6\sin^3 x\cos x+\frac32\sin 4x+6\sin 2x=0$$ |
Тригонометрия | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18138 |
После запуска модели ракеты, ракета выбрасывает ежесекундно газ массой μ = 90 г/с со скоростью u = 300 м/с относительно корпуса. Начальная масса ракеты M = 300 г. Какова наибольшая скорость ракеты, если масса ее топлива равна 200 г. Сопротивлением воздуха пренебречь. Построить графики временных зависимостей скорости и массы ракеты. |
Движение тел с переменной массой | 250₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18139 |
В цилиндре под поршнем находится водяной пар массой m = 10 г при температуре T = 179 °С. Объём цилиндра изотермически уменьшили в β = 3 раза, а давление возросло в α = 1,7 раза. Какие значения имели давление и объём водяного пара перед сжатием? Давление насыщенного пара при температуре 179 °С равно давлению насыщенного пара равно 9,8 атм. |
Молекулярная физика и термодинамика | 100₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18140 |
В цилиндре под поршнем находится m = 80 г неона. Его нагревают на ∆Т = 100 К от первоначальной температуры T1 = 300 К. Этот процесс идёт так, что температура газа меняется пропорционально квадрату давления. Какую работу совершает газ в этом процессе и сколько тепла было к нему подведено? |
Молекулярная физика и термодинамика | 100₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18141 | Молекулярная физика и термодинамика | 100₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 18142 |
Внутри закрытого подвижным поршнем массой m = 9,8 кг цилиндра находится газ. Площадь дна цилиндра S = 10 см2. Первоначально газ занимал объем V0 = 5 л и у него была температура t0 = 0 °С. Сколько теплоты нужно подвести к газу, чтобы нагреть его на ΔТ = 10 K? Если поршень закреплён, то нагрев на ту же температуру при прежних условиях требует подвода Q = 90 Дж. Атмосферное давление снаружи нормальное. Трения нигде нет. |
Молекулярная физика и термодинамика | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18143 |
В калориметре находится 300 г воды при температуре 10 °С. К ней добавили 400 г льда с температурой -20° С. Какая температура будет в смеси? Удельная теплоемкость воды 4,2 кДж/(кг∙К), льда 2,1 кДж/(кг∙К), удельная теплота плавления льда 330 кДж/кг. |
Молекулярная физика и термодинамика | 30₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18144 | Электростатика | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 18145 | Электротехника | 300₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 18146 |
Зависимость радиус-вектора частицы от времени дается законом $$\vec{r}=bt\vec{e}_x-ct^2 \vec{e}_y,$$ где $b$ и $с$ - положительные постоянные. Найти скорость $\vec{V}(t)$ |
Механика | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18147 |
Зависимость угла поворота маховика от времени $$\varphi=A+Bt+Ct^2,$$ где $A$ = 2 рад, $B$ =16 рад/с, $C$ = -2 рад/с2. Момент инерции маховика $J$ = 50 кг∙м2. Найти мощность $P$ в момент $t$ = 3 с. |
Механика | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18148 |
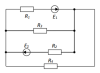
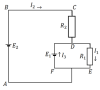
|
Электротехника | 300₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18149 |
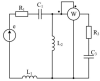
|
Электротехника | 300₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18150 | Электромагнетизм | 11.3 | Физика. Волькенштейн | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 18151 | Электромагнетизм | 11.4 | Физика. Волькенштейн | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 18152 |
Какой вращающий момент действует на рамку с током силой I = 2 А при помещении ее в однородное магнитное поле с индукцией B = 0,2 Tл, если рамка содержит N = 30 витков площадью S = 10 см2, а плоскость рамки образует угол β = 60° с линиями поля? |
Электромагнетизм | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18153 | Электромагнетизм | 75₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 18154 |
Проволочный виток радиусом R = 10 см, по которому течет ток силой l = 20 A (сила тока поддерживается неизменной) свободно установился в однородном магнитном поле. При повороте витка относительно диаметра на угол α = 60° была совершена работа A = 400 мкДж. Найти напряженность поля. |
Электромагнетизм | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18155 |
Проводник, согнутый в виде квадрата со стороной a = 8 см, лежит на столе. Квадрат, потянув за противоположные вершины, вытянули в линию. Определить совершенную при этом работу. Сила тока I = 0,5 A в проводнике поддерживается неизменной. Вертикальная составляющая напряженности магнитного поля Земли HB = 40 A/м. |
Электромагнетизм | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18156 | Теоретическая механика | 300₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 18157 |
Электрон, прошедший ускоряющую разность потенциалов U = 500 В, влетает перпендикулярно силовым линиям в однородное магнитное поле и движется по окружности радиусом R = 10 см. Определить индукцию магнитного поля, период обращения электрона по окружности и момент импульса электрона относительно центра окружности. |
Электромагнетизм | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18158 |
Заряженная частица движется в магнитном поле по окружности со скоростью v=1 Мм/с. Индукция магнитного поля B=0,3 Тл, радиус окружности R=4 см. Найти заряд частицы, если её кинетическая энергия W=12 кэВ. |
Электромагнетизм | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18159 |
Объект наблюдают в микроскоп с красным светофильтром, пропускающим длину волны 645 нм, а затем с зеленым светофильтром при длине волны 490 нм. Во втором случае была использована иммерсионная жидкость – монобромнафталин с показателем преломления 1,66. Апертурный угол объектива микроскопа 65°. Вычислить в обоих случаях предел разрешения микроскопа |
Оптика | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18161 |
Во сколько раз изменится полное сопротивление образца мышечной ткани при измерении его в цепях переменного тока с частотой 10 кГц и 100 кГц? Активное сопротивление ткани 80 Ом, ее электроемкость 0,5 мкФ. |
Биофизика | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18162 |
Квадратный контур, сделанный из провода длиной l = 0,4 м, помещен поперек силовых линий в однородное магнитное поле. Индукция магнитного поля меняется со временем по закону B = 2+0,4t2 мТл. Определить в момент времени t = 2 с магнитный поток, пронизывающий контур, и ЭДС индукции, наведенную в контуре. |
Электромагнетизм | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18163 |
Из урны, содержащей 3 белых и 2 черных шара, наудачу вынули два шара и положили их во вторую урну, содержащую 4 белых и 4 черных шара. Найти вероятность вынуть белый шар из второй урны. |
Теория вероятностей | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18164 |
Задана непрерывная случайная величина $X$ своей функцией распределения $F(x)$. Требуется: |
Теория вероятностей | 100₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18165 |
Нормально распределенная случайная величина X задана своими параметрами a (математическое ожидание) и σ (среднее квадратическое отклонение). Требуется: |
Теория вероятностей | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18166 |
АТС имеет k линий связи. Поток вызовов - простейший с интенсивностью λ вызовов в минуту. Среднее время переговоров составляет t минут. Время переговоров распределено по показательному закону. Найти: |
Математическая статистика | 100₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18167 |
Данные наблюдений над двумерной случайной величиной (X,Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X. Выполнить чертеж.
|
Математическая статистика | 100₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18168 |
Известно эмпирическое распределение выборки объема n случайной величины X. Проверить гипотезу о распределении по закону Пуассона генеральной совокупности этой величины. Использовать критерий согласия Пирсона (хи-квадрат) при уровне значимости α = 0,05.
|
Математическая статистика | 100₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18169 |
Батарея аккумуляторов с ЭДС E = 24 В и внутренним сопротивлением r = 0,01 Ом соединена с потребителем двумя медными проводами, расположенными на расстоянии d = 5 см один от другого. Провода закреплены на изоляторах, расстояние между которыми l1 = 0,5 м. Определить силу, действующую на изоляторы при коротком замыкании на зажимах потребителя, если длина подводящей линии 20 м, а сечение проводов 3 мм2. Удельное сопротивление меди равно 1,72∙10-8 Ом∙м. Построить картину силовых линий индукции магнитного поля. |
Электромагнетизм | 200₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18170 | Постоянный ток | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 18171 |
Вычислить объём тела, образованного вращением фигуры, ограниченной графиками функций вокруг оси OX, сделать чертёж: $$y=-4x^3;x=0;y=4$$ |
Определенный интеграл | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18172 |
Дано скалярное поле $u=u(x; y)$:
|
Дифференциальное исчисление функций нескольких переменных | 100₽ | |||||||||||||||||||||||||||||||||||||||||||||
| 18173 |
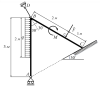
Автомобиль преодолевает подъём с углом наклона α. Коэффициент трения колёс о дорогу равен f. Определить тормозной путь автомобиля, если его скорость в момент отключения двигателя и включения тормозного привода была равна v0. Колёса автомобиля считать полностью заторможенными. |
Кинематика | 150₽ |