Если найти нужную задачу не удаётся, Вы можете оформить Заказ.
Как использовать поиск
| Номер | Условие задачи | Предмет | Задачник | Цена | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 18029 |
Разложить в ряд Тейлора по степеням $(x-2)$ функцию $$y=(2+x)^{-1/2}$$ |
Ряды | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18030 |
Функцию $$f(x)=\sin \frac{x}{2}$$ разложить в ряд Фурье в интервале $(-\pi; \pi)$. |
Ряды | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18031 |
Во сколько раз уменьшится потенциал покоя клетки, если отношение концентрации калия внутри клетки к концентрации калия во внеклеточной среде уменьшится в 2 раза? Начальное отношение концентраций равно 52. |
Биофизика | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18032 |
Искусственный спутник Земли описывает круговую орбиту радиуса R на небольшой высоте над поверхностью Земли (изменением силы тяжести на этой высоте по сравнению с силой тяжести на поверхности Земли можно пренебречь). Определить скорость движения спутника по орбите и время одного оборота спутника. Радиус Земли R= 6380 км. |
Механика | 100₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18033 |
ПЕРВАЯ ЗАДАЧА ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ |
Механика | 300₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18034 |
Найти общее решение системы линейных дифференциальных уравнений. Сделать проверку найденного решения подстановкой в исходную систему: |
Дифференциальные уравнения | 100₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18035 |
Решить дифференциальное уравнение второго порядка: |
Дифференциальные уравнения | 100₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18036 |
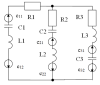
1. ЗАДАНИЕ НА ВЫПОЛНЕНИЕ РАСЧЕТА
Таблица 1.2. Наличие ЭДС в ветвях расчетной схемы
Таблица 1.3. Наличие активных и реактивных сопротивлений в ветвях расчетной схемы
Задача решена с помощью комплексных чисел. Для построения лучевой диаграммы токов и векторной диаграммы напряжений использовали графический калькулятор Desmos. |
Электротехника | 300₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18037 |
Решить дифференциальное уравнение второго порядка: |
Дифференциальные уравнения | 100₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18038 |
В лотерее 100 билетов, среди них один выигрыш в 50 рублей, 3 – по 25 рублей, 6 – по 10 рублей, 15 – по 3 рубля. Некто покупает один билет. Найти вероятность какого-нибудь выигрыша. |
Теория вероятностей | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18039 |
Два стрелка A и B по очереди стреляют в одну мишень. Вероятность попадания при каждом выстреле равна 0,25. Каждый стрелок имеет право произвести два выстрела, однако стрельба прекращается, когда кто-нибудь из них попадёт в мишень. Определить вероятность поражения мишени каждым стрелком в отдельности. |
Теория вероятностей | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18040 |
Детали проходят три операции обработки. Вероятность появления брака во время первой операции равна 0,02, второй – 0,03, третьей – 0,02. Найти вероятность выхода стандартной детали. |
Теория вероятностей | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18041 |
Положительное число $x \neq \frac12, \frac{1}{20}$, таково, что $$\log_{20x} (45x)=\log_{2x} (33x)=\log_{10}a$$ Найдите a. Если необходимо, округлите ответ с точностью до 0,01. |
Алгебра | 250₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18042 |
При каких значениях $a$ уравнение $$\sin^2 {3x} -(a+\frac12)\sin{3x}+\frac{a}{2}=0$$ имеет ровно три корня на отрезке $\left[\frac{2\pi}{3};\pi\right]$? |
Тригонометрия | 100₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18043 |
Решить уравнение $$2\sin \left( 3x+\frac{\pi}{4} \right) = \sqrt{1+8\sin {2x} \cos^2 {2x} }$$ |
Тригонометрия | 250₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18044 |
Решить неравенство $$(3-\cos^2 x-2\sin x)(\lg^2 y+2\lg y+4)\le 3$$ |
Тригонометрия | 250₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18045 |
В каждой из двух урн содержится 4 черных и 6 белых шаров. Из второй урны наудачу извлечен один шар и переложен в первую урну, после чего из первой урны наудачу извлечён шар. Найти вероятность того, что шар, извлечённый из первой урны, окажется белым. |
Теория вероятностей | 100₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18046 |
В цехе три группы автоматических станков (по степеням амортизации) производят одни и те же детали. Производительность их одинакова, но качество работы различно. Известно, что станки первой группы производят 0,8 деталей первого сорта, второй – 0,85, третьей – 0,9. Все произведённые в цехе за смену детали в не рассортированном виде сложены на складе. Взятая со склада наудачу деталь оказалась первого сорта. На станке какой группы вероятнее всего она была изготовлена, если станков первой группы 5 штук, второй – 4 шт. и третьей – 2 шт.? |
Теория вероятностей | 100₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18047 |
Выполните действия над комплексными числами и запишите результат в тригонометрической и показательной формах: $$\frac{2+i}{4+2i}+\frac{i}{5-6i}$$ |
Теория функций комплексного переменного | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18048 |
Найти неопределённый интеграл. Результаты проверить дифференцированием: $$ \int (x+2)\cos(x^2+4x+1)dx$$ |
Неопределённый интеграл | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18049 |
Найти неопределённый интеграл. Результаты проверить дифференцированием: $$ \int \frac{x\cos x dx}{\sin^3 x}$$ |
Неопределённый интеграл | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18050 |
Найти полный дифференциал функции двух переменных: $$f(x;y)=2xy^3-4x^3 y-y^4$$ |
Дифференциальное исчисление функций нескольких переменных | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18051 |
Вычислить по формуле Ньютона-Лейбница определенный интеграл: $$\int_0^1 \frac{dx}{1+\sqrt[3]{x}}$$ |
Определенный интеграл | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18052 |
Найти решение уравнения, удовлетворяющее начальному условию: $$y'y=2x-3, \ y(1)=0$$ |
Дифференциальные уравнения | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18053 |
Найти общее и частное решение дифференциального уравнения, удовлетворяющее начальному условию: $$y''+4y'+4y=\sin 3x, \ y(0)=2; y'(0)=1$$ |
Дифференциальные уравнения | 100₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18054 |
Выяснить, какие из данных рядов сходятся и какие расходятся: $$\sum_{n=1}^{\infty} \frac{n^3}{(2n)!}$$ |
Ряды | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18055 |
Найти область сходимости степенного ряда $$\sum_{n=1}^{\infty}\frac{n-1}{3^n(n+2)}x^n$$ |
Ряды | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18056 |
Разложить функцию $f(x)$ в ряд Фурье в указанном интервале. Выписать полученный ряд и три первых члена разложения отдельно. Построить графики функции $f(x)$ и её приближения: $$f(x)=x-3 \ в \ интервале \ (-\pi;\pi)$$ |
Ряды | 150₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18057 |
Выполните действия над комплексными числами и запишите результат в тригонометрической и показательной формах $$ \frac{i}{2+i}-\frac{5+7i}{3-i} $$ |
Теория функций комплексного переменного | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18058 |
Найти неопределённый интеграл. Результаты проверить дифференцированием: $$\newcommand{\tg}{\mathop{\mathrm{tg}}\nolimits}\int \frac{dx}{\cos x\sqrt{2+5\tg^2 x}}$$ |
Неопределённый интеграл | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18059 |
Найти неопределённый интеграл. Результаты проверить дифференцированием: $$\int{\sin(2x)\ln(\cos(x)) }dx$$ |
Неопределённый интеграл | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18060 |
Найти полный дифференциал функции двух переменных: $$f(x;y)=4x^5-3x^2y^3-6y^5 $$ |
Дифференциальное исчисление функций нескольких переменных | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18061 |
Вычислить по формуле Ньютона-Лейбница определенный интеграл: $$\int_1^4 \frac{e^{\sqrt{x}}dx}{\sqrt{x}{x}}$$ |
Определенный интеграл | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18062 |
Найти решение уравнения, удовлетворяющее начальному условию: $$ y'=(4-3y)^2 x,\ y(0)=1 $$ |
Дифференциальные уравнения | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18063 |
Найти общее и частное решение дифференциального уравнения, удовлетворяющее начальному условию: $$y''-4y'+5y=-x^2+1,\ y(0)=0;\ y' (0)=2 $$ |
Дифференциальные уравнения | 100₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18064 |
|
Механика | 250₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18065 |
Два вагона массами m, двигающиеся навстречу друг другу со скоростями v1 и v2, сталкиваются и останавливаются. При этом происходит сжатие пружин буферов вагонов на величину x. Под действием силы F0 пружина сжимается на x0. Сжатие пружины пропорционально силе. Определить величины, указанные в таблице знаком вопроса.
|
Механика | 250₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18066 |
|
Механика | 250₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18067 |
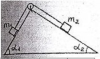
Человек массой m1 прыгает с неподвижной тележки, стоящей на рельсах, вдоль рельсов. При этом тележка массой m2 откатывается в противоположную сторону на расстояние S. Коэффициент трения тележки о рельсы μ. Энергия, затраченная человеком при прыжке ∆W. Определить величины, указанные в таблице знаком вопроса.
|
Механика | 200₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18068 |
Маховик в виде диска массой m, радиусом R, момент инерции которого равен J, находится в состоянии покоя. Под действием приложенных сил маховик начинает вращаться. Работа, совершаемая внешними силами, равна A. Момент внешних сил равен M, частота вращения ν. Кинетическая энергия маховика через t секунд равна Ek. Определить величины, указанные в таблице знаком вопроса.
|
Механика | 200₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18069 |
Один моль идеального газа переходит из начального состояния 1 в конечное состояние 3 в результате двух изопроцессов 1-2 и 2-3. Значения давления и объема газа в состояниях 1 и 3 равны соответственно p1, V1 и p3, V3. Найти давление, объем и температуру газа p2, V2, T2 в промежуточном состоянии 2. Изобразить процессы в координатах p-V, p-T и V-T.
|
Молекулярная физика и термодинамика | 200₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18093 |
Найти все значения параметра a, при каждом из которых уравнение $$x^2-x+a^3-1=0$$ имеет один положительный корень. В ответе укажите наибольшее целое a. |
Алгебра | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18094 |
КПД паровой машины составляет k = 40% =0.4 от КПД тепловой машины, работающей по циклу Карно между теми же температурами. Температура пара, поступающего из котла в паровую машину T1 = 250+273°C=523K, температура конденсатора T2 = 90+273°C=363 K. Определить (в МВт) мощность паровой машины, если она потребляет за t = 12 часов = 43200 c Qпол =10 ТДж = 1∙1013 Дж энергии. |
Молекулярная физика и термодинамика | 60₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18095 |
Определить скорость велосипедиста, если при повороте по кругу радиусом r = 10 м он отклонился на α = 15° от вертикали |
Механика | 60₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18096 |
Платформа длиной L = 20м и массой M = 200 кг движется со скоростью v1 = 6,0 м/с по горизонтальным рельсам без трения. Человек массой m = 75 кг начинает движение из одного конца платформы к другому в направлении ее движения со скоростью v2 = 2,5 м/с относительно платформы. На какое расстояние переместится платформа за то время, которое требуется человеку для перехода из одного ее конца до другого? |
Механика | 60₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18097 |
Четыре друга ходили в лес за грибами. Вернувшись, каждые двое из них посчитали, сколько грибов они собрали в сумме. Получились числа 7, 9, 10, 10, 11, 13. Сколько грибов собрал каждый? |
Алгебра | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18098 |
Найдите натуральное число п такое, что числа n + 15 и n - 14 являются квадратами других чисел, |
Алгебра | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18100 | Механика | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18121 |
Вычислить интеграл по формуле Ньютона-Лейбница $$\int_1^3 \frac{dx}{\sqrt{9-4x^2}}$$ |
Определенный интеграл | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18122 |
Дифференциальное уравнение $$ (1+y)y''-5(y' )^2=0$$. |
Дифференциальные уравнения | 50₽ |