|
17896 |
Вычислить несобственный интеграл, используя вычеты: $$\int\limits_{-\infty}^{+\infty} \frac{x\sin {x}}{x^2+4x+20}dx$$
|
Теория функций комплексного переменного |
|
|
150₽ |
|
|
12140 |
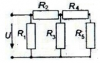
САМОСТОЯТЕЛЬНАЯ РАБОТА 1
Вариант 91.
Расчёт разветвлённой электрической цепи постоянного тока
Для данной электрической цепи определить с использованием законов Ома и Кирхгофа
1. Токи в ветвях
2. Мощность, развиваемую источником энергии, и мощность потребителей
3. Составить баланс мощности
| Последняя цифра номера студенческого билета |
U, В |
R1, Ом |
R2, Ом |
R2, Ом |
R4, Ом |
R5, Ом |
| 1 |
36 |
10 |
7 |
5 |
5 |
9 |
|
Электротехника |
91 |
Разветвлённая электрическая цепь постоянного тока |
150₽ |
|
|
14160 |
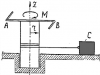
Вал кабестана (механизма для перемещения грузов) радиусом r приводится в движение постоянным вращающим моментом М, приложенным к рукоятке АВ. Определить ускорение груза массой m, если коэффициент трения скольжения груза о горизонтальную плоскость равен f. Момент инерции кабестана относительно оси вращения равен Jz. Массой каната пренебречь
|
Теоретическая механика |
Д7.11 |
Теоретическая механика 2 |
150₽ |
|
|
11722 |
Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям: $$J[y]=\int_{-1}^{0}(12xy-{y'}^2)dx; y(-1)=1,\ y(0)=0$$
|
Вариационное исчисление |
2.17 |
Вариационное исчисление |
150₽ |
|
|
14166 |
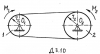
Два шкива радиусами r1 и r2 и массами m1 и m2, соединенные ремнем, вращаются вокруг параллельных осей О1 и О2. Найти угловое ускорение шкива 1, если к нему приложен вращающий момент М1, а к шкиву 2 приложен момент сопротивления М2. Шкивы считать однородными дисками. Скольжением ремня и его массой пренебречь.
|
Теоретическая механика |
D3.10 |
МИИТ. Теоретическая механика. 2012 год |
150₽ |
|
|
4277 |
Наэлектризованный шар радиусом имеет объемную плотность заряда ρ. Сила, действующая на точечный заряд q, находящийся на расстоянии d от поверхности шара равна F. Определите величину, обозначенную в таблице знаком вопроса, энергию взаимодействия заряда и шара и начертите графики зависимости напряженности и потенциала шара от расстояния до его центра.
| q∙10-4 Кл |
ρ∙10-4 Кл/м3 |
r, см |
d, см |
F, мкН |
| 40 |
60 |
8 |
? |
590 |
|
Электростатика |
|
|
150₽ |
|
|
16258 |
По обмотке тороида с ненамагниченным железным сердечником пустили ток силой 0,6 А. Витки провода диаметром 0,4 мм плотно прилегают друг к другу. Определить индуктивность тороида при данных условиях, а также энергию магнитного ноля в сердечнике, если площадь его сечения 4 см2, а диаметр средней линии 30 см.
|
Электромагнетизм |
|
|
150₽ |
|
|
13522 |
Один моль идеального газа совершает процесс, в котором давление газа P убывает с увеличением его объема V по заданному закону P(V). Найти максимальную температуру газа в этом процессе.
| № варианта |
P(V) |
| 20 |
P(V) = P0e-bV, P0 = 2∙105 Па, b = 25 м-3 |
|
ФИЗИКА |
4-3-20 |
ТГУ. Практические занятия по физике. 2019 год |
150₽ |
|
|
17865 |
Вычислить интеграл $$\oint\limits_{|z-i|=1} \frac{e^z dz}{z^4+2z^2+1}$$
|
Теория функций комплексного переменного |
|
|
150₽ |
|
|
10452 |
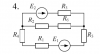
Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии.
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 2, выполнить следующее:
1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений не следует.
2. Определить токи в ветвях методом контурных токов.
3. Определить режимы работы активных элементов и составить баланс мощностей.
Значения ЭДС источников и сопротивлений приемников приведены в табл. 2.
| Предпоследняя цифра учебного шифра студента |
E1, В |
E2, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 9 |
140 |
120 |
8 |
16 |
12 |
20 |
15 |
10 |
|
Электротехника |
294 |
МИИТ. Общая электротехника и электроника. 2016 год |
150₽ |
|
|
10532 |
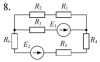
Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии.
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 2, выполнить следующее:
1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений не следует.
2. Определить токи в ветвях методом контурных токов.
3. Определить режимы работы активных элементов и составить баланс мощностей.
Значения ЭДС источников и сопротивлений приемников приведены в табл. 2.
| Предпоследняя цифра учебного шифра студента |
E1, В |
E2, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 8 |
130 |
130 |
15 |
11 |
21 |
14 |
8 |
16 |
|
Электротехника |
288 |
МИИТ. Общая электротехника и электроника. 2016 год |
150₽ |
|
|
12898 |
Диск массой m, имеющий радиус R, начинает вращаться под действием силы F, приложенной по касательной к образующей диска, перпендикулярно ею радиусу; при этом момент сил трения, действующий на диск, равен М1. За время t, отсчитанное oт начала движения, диск совершает N оборотов. Определить параметр, обозначенный в таблице данных для Вашего варианта знаком «?».
| Номер варианта |
m, кг |
R, м |
F, Н |
M1, Н∙м |
t, сек |
N |
| 2 |
4 |
? |
12 |
4 |
15 |
7 |
|
Механика |
5-2 |
ЗабГУ. Физика. 2011 год |
150₽ |
|
|
11738 |
Найти все экстремали функционала $J(y)$: $$J[y]=\int_{0}^{\pi}({y'}^2+y^2-4y\sin x)dx,$$ удовлетворяющие граничным условиям $y(0)=0;\ y(\pi)=\frac{e^\pi-e^{-\pi}}{2}$
|
Вариационное исчисление |
2.30 |
Вариационное исчисление |
150₽ |
|
|
11820 |
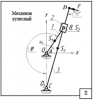
1. Структурный анализ механизма
1.1 Начертить схему механизма в масштабе k1 для заданного углом ψ мгновенного положения входного (ведущего) звена. Построение следует начинать с точки О, откладывая угол φ от оси ОХ или ОУ в сторону вращения ведущего звена механизма;
1.2 Определить количество звеньев и кинематических пар механизма, обозначить на схеме входное (ведущее) звено цифрой 1 и стойку (неподвижное звено) цифрой 0 (кинематические пары обозначают заглавными буквами);
1.3 Определить степень подвижности W механизма и выделить входящую в него структурную группу Ассура, указав класс, порядок и вид группы.
2. Кинематический анализ механизма в положении, заданном углом φ.
2.1. Построить планы скоростей для всех указанных на схеме механизма точек. При расчете принять ω1 = const.
2.2. Определить величины и направления угловых скоростей ωi звеньев (где i = 1, 2, 3, …− порядковый номер звена). Направления угловых скоростей указать на кинематической схеме механизма круговыми стрелками.
2.3 При определении скоростей и ускорений центров масс Si звеньев принять, что центр массы звена расположен на середине его длины. Центр массы ползуна принять совпадающим с центром шарнира.
Дано: ω1 = 40 рад/с, φ = 30 град, lAB = 0,12 м, lAC = 0,3 м, lCD = 0,45 м.
|
Теоретическая механика |
|
|
150₽ |
|
|
10306 |
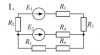
Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии.
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 2, выполнить следующее:
1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений не следует.
2. Определить токи в ветвях методом контурных токов.
3. Определить режимы работы активных элементов и составить баланс мощностей.
Значения ЭДС источников и сопротивлений приемников приведены в табл. 2.
| Предпоследняя цифра учебного шифра студента |
E1, В |
E2, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 8 |
130 |
130 |
15 |
11 |
21 |
14 |
8 |
16 |
|
Электротехника |
281 |
МИИТ. Общая электротехника и электроника. 2016 год |
150₽ |
|
|
14266 |
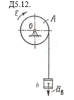
На однородный цилиндр A массой m1 радиусом r намотана нить, на конце которой подвешен груз b массой m2. Определить закон изменения угловой скорости, если груз опускается вниз из состояния покоя.
|
Теоретическая механика |
Д5.12 |
Теоретическая механика 2 |
150₽ |
|
|
13538 |
Один моль идеального газа переходит из начального состояния 1 в конечное состояние 3 в результате двух процессов 1-2 и 2-3. Значения давления и объема газа в состояниях 1 и 3 равны соответственно P1, V1 и P3, V3. Найти работу, совершенную газом, количество теплоты Q, полученное газом и приращение внутренней энергии газа ΔU в процессе перехода из начального состояния 1 в конечное состояние 3.
| № варианта |
газ, процессы, P1, V1, P3, V3 |
| 8 |
изотермический 1-2, газ - N2, P1 = 105 Па, V1 = 3 л, изобарный 2-3, P3 = 2∙105 Па, V3 = 6 л |
|
ФИЗИКА |
5-1-8 |
ТГУ. Практические занятия по физике. 2019 год |
150₽ |
|
|
17873 |
Вычислить интеграл $$\oint\limits_{ |z|=3} \frac{\sin{z}\ dz}{z^2(z-1)^2} $$
|
Теория функций комплексного переменного |
|
|
150₽ |
|
|
9182 |
Найти экстремали функционалов: с дифференциальными связями:
$$J[y_1,y_2]=\int_0^1({y_1'}^2-2{y_2'}^2+y_2^2)dx;$$
$$y_1(0)=0, y_1(\pi/2)=1, y_2(0)=0, y_2(\pi/2)=\pi/2, y_1-y'_2=0$$
|
Вариационное исчисление |
4.16 |
Вариационное исчисление |
150₽ |
|
|
10468 |
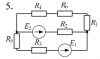
Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии.
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 2, выполнить следующее:
1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений не следует.
2. Определить токи в ветвях методом контурных токов.
3. Определить режимы работы активных элементов и составить баланс мощностей.
Значения ЭДС источников и сопротивлений приемников приведены в табл. 2.
| Предпоследняя цифра учебного шифра студента |
E1, В |
E2, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 7 |
120 |
140 |
10 |
8 |
13 |
20 |
15 |
21 |
|
Электротехника |
275 |
МИИТ. Общая электротехника и электроника. 2016 год |
150₽ |
|
|
10548 |
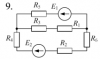
Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии.
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 2, выполнить следующее:
1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений не следует.
2. Определить токи в ветвях методом контурных токов.
3. Определить режимы работы активных элементов и составить баланс мощностей.
Значения ЭДС источников и сопротивлений приемников приведены в табл. 2.
| Предпоследняя цифра учебного шифра студента |
E1, В |
E2, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 6 |
110 |
150 |
17 |
12 |
9 |
14 |
20 |
15 |
|
Электротехника |
269 |
МИИТ. Общая электротехника и электроника. 2016 год |
150₽ |
|
|
12914 |
Диск массой m, имеющий радиус R, начинает вращаться под действием силы F, приложенной по касательной к образующей диска, перпендикулярно ею радиусу; при этом момент сил трения, действующий на диск, равен М1. За время t, отсчитанное oт начала движения, диск совершает N оборотов. Определить параметр, обозначенный в таблице данных для Вашего варианта знаком «?».
| Номер варианта |
m, кг |
R, м |
F, Н |
M1, Н∙м |
t, сек |
N |
| 10 |
20 |
0,4 |
8 |
? |
10 |
6 |
|
Механика |
5-10 |
ЗабГУ. Физика. 2011 год |
150₽ |
|
|
15074 |
По тонкой нити, изогнутой по дуге окружности радиусом R равномерно распределён заряд Q. На точечный заряд q, находящийся в центре дуги, составляющей 1/4 часть полной окружности, действует сила F. Определить параметр, обозначенный в таблице для Вашего варианта знаком «?».
| Вариант |
R, м |
Q, нКл |
q, нКл |
n |
F, мкН |
| 8 |
0,4 |
400 |
? |
1/2 |
114,5 |
|
Электростатика |
2-1-3 |
|
150₽ |
|
|
10322 |
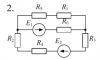
Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии.
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 2, выполнить следующее:
1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений не следует.
2. Определить токи в ветвях методом контурных токов.
3. Определить режимы работы активных элементов и составить баланс мощностей.
Значения ЭДС источников и сопротивлений приемников приведены в табл. 2.
| Предпоследняя цифра учебного шифра студента |
E1, В |
E2, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 7 |
120 |
140 |
10 |
8 |
13 |
20 |
15 |
21 |
|
Электротехника |
272 |
МИИТ. Общая электротехника и электроника. 2016 год |
150₽ |
|
|
13162 |
Средняя плотность планеты равна ρ, ее радиус – R, период обращения планеты вокруг своей оси – T. Найти вес тела массой m на экваторе планеты.
| № варианта |
ρ, R, T, m |
| 2 |
ρ = 2,8∙103 кг/м3, R = 1,2∙105 м, T = 1,2∙104 с, m = 10 кг |
|
ФИЗИКА |
2-2-2 |
ТГУ. Практические занятия по физике. 2019 год |
150₽ |
|
|
13554 |
Один моль идеального газа переходит из начального состояния 1 в конечное состояние 3 в результате двух процессов 1-2 и 2-3. Значения давления и объема газа в состояниях 1 и 3 равны соответственно P1, V1 и P3, V3. Найти работу, совершенную газом, количество теплоты Q, полученное газом и приращение внутренней энергии газа ΔU в процессе перехода из начального состояния 1 в конечное состояние 3.
| № варианта |
газ, процессы, P1, V1, P3, V3 |
| 16 |
изобарный 1-2, газ - He, P1 = 105 Па, V1 = 3 л, изохорный 2-3, P3 = 2∙105 Па, V3 = 6 л |
|
ФИЗИКА |
5-1-16 |
ТГУ. Практические занятия по физике. 2019 год |
150₽ |
|
|
17881 |
Вычислить интеграл $$\oint\limits_{\frac{x^2}{4}+\frac{y^2}{9}=1} \frac{z}{(z-1)^2(z-3) }$$
|
Теория функций комплексного переменного |
|
|
150₽ |
|
|
4373 |
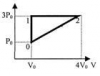 Один киломоль идеального одноатомного газа (например, гелия) участвует в тепловом цикле 0-1-2-0. Найти работу, совершенную газом за цикл, а также К.П.Д. цикла. Температура газа в состоянии 0 равна 150 К. Напомним, что К. .П. Д. цикла равен отношению работы, совершенной газом за цикл, к полученному при этом количеству тепла. Один киломоль идеального одноатомного газа (например, гелия) участвует в тепловом цикле 0-1-2-0. Найти работу, совершенную газом за цикл, а также К.П.Д. цикла. Температура газа в состоянии 0 равна 150 К. Напомним, что К. .П. Д. цикла равен отношению работы, совершенной газом за цикл, к полученному при этом количеству тепла.
|
Молекулярная физика и термодинамика |
|
|
150₽ |
|
|
10484 |
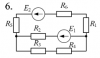
Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии.
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 2, выполнить следующее:
1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений не следует.
2. Определить токи в ветвях методом контурных токов.
3. Определить режимы работы активных элементов и составить баланс мощностей.
Значения ЭДС источников и сопротивлений приемников приведены в табл. 2.
| Предпоследняя цифра учебного шифра студента |
E1, В |
E2, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 5 |
100 |
160 |
10 |
14 |
9 |
11 |
15 |
11 |
|
Электротехника |
256 |
МИИТ. Общая электротехника и электроника. 2016 год |
150₽ |
|
|
6194 |
В процессе политропного сжатия воздуха G = 62∙103 кг/с, в одноступенчатом поршневом компрессоре отводится теплота в количестве Q = 1350 Дж/с. При сжатии от начального абсолютного давления p1 = 0,1∙106 Па температура воздуха возрастает от T1 = 288 К до T2 = 383 К. Определить показатель политропы процесса сжатия, конечное давление, удельную работу сжатия и техническую работу на получение сжатого воздуха, Дж/кг. Какова теоретически потребная мощность привода компрессора, кВт.
Дано: G = 62∙103 кг/ч; Q = 1,35 кДж/с; p1 = 0,1∙106 Па; T1 = 288 К; T2 = 383 К.
|
Теплотехника |
|
|
150₽ |
|
|
10564 |
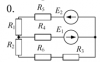
Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии.
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 2, выполнить следующее:
1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений не следует.
2. Определить токи в ветвях методом контурных токов.
3. Определить режимы работы активных элементов и составить баланс мощностей.
Значения ЭДС источников и сопротивлений приемников приведены в табл. 2.
| Предпоследняя цифра учебного шифра студента |
E1, В |
E2, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 4 |
90 |
170 |
6 |
11 |
15 |
20 |
12 |
13 |
|
Электротехника |
240 |
МИИТ. Общая электротехника и электроника. 2016 год |
150₽ |
|
|
12930 |
Диск массой m, имеющий радиус R, начинает вращаться под действием силы F, приложенной по касательной к образующей диска, перпендикулярно ею радиусу; при этом момент сил трения, действующий на диск, равен М1. За время t, отсчитанное oт начала движения, диск совершает N оборотов. Определить параметр, обозначенный в таблице данных для Вашего варианта знаком «?».
| Номер варианта |
m, кг |
R, м |
F, Н |
M1, Н∙м |
t, сек |
N |
| 18 |
60 |
0,6 |
20 |
8 |
45 |
? |
|
Механика |
5-18 |
ЗабГУ. Физика. 2011 год |
150₽ |
|
|
16738 |
На железнодорожной платформе у начала второго вагона покоящегося поезда стоял пассажир. Поезд тронулся с места и далее двигался равноускоренно. При этом оказалось, что третий вагон поезда проезжал мимо пассажира в течение времени τ. В течение какого времени будет проезжать мимо пассажира пятый вагон? Вагоны поезда пронумерованы по порядку с начала поезда и имеют одинаковую длину. Пассажир неподвижен.
|
Кинематика |
|
|
150₽ |
|
|
10340 |
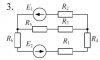
Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии.
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 2, выполнить следующее:
1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений не следует.
2. Определить токи в ветвях методом контурных токов.
3. Определить режимы работы активных элементов и составить баланс мощностей.
Значения ЭДС источников и сопротивлений приемников приведены в табл. 2.
| Предпоследняя цифра учебного шифра студента |
E1, В |
E2, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 3 |
80 |
180 |
11 |
7 |
12 |
16 |
21 |
13 |
|
Электротехника |
233 |
МИИТ. Общая электротехника и электроника. 2016 год |
150₽ |
|
|
13178 |
Средняя плотность планеты равна ρ, ее радиус – R, период обращения планеты вокруг своей оси – T. Найти вес тела массой m на экваторе планеты.
| № варианта |
ρ, R, T, m |
| 10 |
ρ = 2,4∙103 кг/м3, R = 1,2∙105 м, T = 1,2∙104 с, m = 10 кг |
|
ФИЗИКА |
2-2-10 |
ТГУ. Практические занятия по физике. 2019 год |
150₽ |
|
|
14388 |
Шлюпка массой 180 кг спущена на воду с борта судна, идущего со скоростью 3,0 м/с. Какое расстояние пройдёт шлюпка, пока её скорость не уменьшится в 10 раз? Насколько отстанет она от судна за это время? Сопротивления воды изменяется по закону $\vec{F}=-k_c\vec{v}$, где F - сила сопротивления, действующая на шлюпку, Н; kc = 90 Н∙с/м - коэффициент пропорциональности; v - скорость, м/с.
|
Механика |
|
|
150₽ |
|
|
11706 |
Чему равен угол α между главными плоскостями поляризатора и анализатора, если интенсивность естественного света, прошедшего через анализатор и поляризатор, уменьшается в 4 раза? Коэффициент поглощения света в каждом поляроиде равен k = 10%.
|
Оптика |
|
|
150₽ |
|
|
14944 |
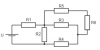
Найти силу тока, протекающего через источник напряжения в 12 В, если R1 = 5 Ом, R2 = 7 Ом, R3 = 9 Ом, R4 = 12 Ом, R5 = 1 Ом, R6 = 3 Ом
|
Постоянный ток |
103 |
Разветвлённая электрическая цепь постоянного тока |
150₽ |
|
|
13194 |
Средняя плотность планеты равна ρ, ее радиус – R, период обращения планеты вокруг своей оси – T. Найти вес тела массой m на экваторе планеты.
| № варианта |
ρ, R, T, m |
| 18 |
ρ = 1,6∙103 кг/м3, R = 8,2∙104 м, T = 1,7∙104 с, m = 30 кг |
|
ФИЗИКА |
2-2-18 |
ТГУ. Практические занятия по физике. 2019 год |
150₽ |
|
|
18190 |
В электростатическом поле, образованном системой распределённых электрических зарядов, потенциал электростатического поля φ меняется по известному закону φ = f(x, y, z). Найти напряжённость поля в точках x1, y1, z1. Охарактеризовать картину эквипотенциальных поверхностей.
| № |
Закон изменения потенциала φ = f(x,y,z), В |
Постоянные |
x1, м |
y1, м |
z1, м |
| a |
b |
| 21 |
$\varphi=a(x^2+y^2)-bz^2$ |
6 м2/В |
2 м2/В |
2 |
2 |
2 |
|
Электростатика |
|
|
150₽ |
|
|
10436 |
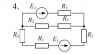
Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии.
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 2, выполнить следующее:
1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений не следует.
2. Определить токи в ветвях методом контурных токов.
3. Определить режимы работы активных элементов и составить баланс мощностей.
Значения ЭДС источников и сопротивлений приемников приведены в табл. 2.
| Предпоследняя цифра учебного шифра студента |
E1, В |
E2, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 1 |
60 |
200 |
11 |
18 |
13 |
19 |
14 |
8 |
|
Электротехника |
214 |
МИИТ. Общая электротехника и электроника. 2016 год |
150₽ |
|
|
9230 |
Найти экстремали функционалов в изопериметрической задаче:
$$J[y]=\int_0^1(y-{y'}^2)dx$$ $$y(0)=0, y(1)=1/4,\ \int_0^1{y'}^2dx=1/12$$
|
Вариационное исчисление |
4.23 |
Вариационное исчисление |
150₽ |
|
|
11966 |
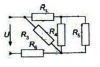
САМОСТОЯТЕЛЬНАЯ РАБОТА 1
Вариант 15.
Расчёт разветвлённой электрической цепи постоянного тока
Для данной электрической цепи определить с использованием законов Ома и Кирхгофа
1. Токи в ветвях
2. Мощность, развиваемую источником энергии, и мощность потребителей
3. Составить баланс мощности
| Последняя цифра номера студенческого билета |
U, В |
R1, Ом |
R2, Ом |
R2, Ом |
R4, Ом |
R5, Ом |
| 5 |
90 |
10 |
14 |
12 |
9 |
13 |
|
Электротехника |
15 |
Разветвлённая электрическая цепь постоянного тока |
150₽ |
|
|
13984 |
Сила тяги трамвайного вагона массой m в период разгона возрастает пропорционально времени, увеличиваясь на k [Н] в течение каждой секунды. Найти уравнение движения вагона, если его сопротивление движению постоянно и равно f [Н].
|
Теоретическая механика |
Д2.13 |
Теоретическая механика 2 |
150₽ |
|
|
16830 |
С помощью рассуждений докажите, что
а) $\overline{A\cup B}=\overline{A} \cap \overline{B}$,
б) $\left(A\backslash B\right)\cup \left(A\backslash C\right)=A\backslash \left(B\cap C\right)$,
в) $A\cap \left(B\cup C\right)=\left(A\cap B\right)\cup \left(A\cap C\right)$.
|
Математическая логика |
|
|
150₽ |
|
|
12064 |
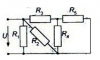
САМОСТОЯТЕЛЬНАЯ РАБОТА 1
Вариант 56.
Расчёт разветвлённой электрической цепи постоянного тока
Для данной электрической цепи определить с использованием законов Ома и Кирхгофа
1. Токи в ветвях
2. Мощность, развиваемую источником энергии, и мощность потребителей
3. Составить баланс мощности
| Последняя цифра номера студенческого билета |
U, В |
R1, Ом |
R2, Ом |
R2, Ом |
R4, Ом |
R5, Ом |
| 6 |
50 |
8 |
11 |
9 |
7 |
14 |
|
Электротехника |
56 |
Разветвлённая электрическая цепь постоянного тока |
150₽ |
|
|
16010 |
Частица, получившая запас кинетической энергии после прохождения разности потенциалов ∆ϕ, влетает в однородное магнитное поле со скоростью v, составляющей угол α с линиями вектора индукции магнитного поля В, после чего двигается по спирали радиусом R и шагом h. Определить параметры, обозначенные в таблице для Вашего варианта знаком «?».
| Тип частицы |
Масса частицы, кг |
Заряд частицы, Кл |
| e |
9,1∙10-31 |
-1,6∙10-19 |
| p |
1,672∙10-27 |
1,6∙10-19 |
| α |
6,64∙10-27 |
3,2∙10-19 |
.
| Вариант |
Тип частицы |
∆ϕ, В |
v, м/с |
В, Тл |
α, град |
R, мм |
h, мм |
| 9 |
α |
1500 |
? |
1,0 |
45 |
? |
70,11 |
|
Электродинамика |
|
|
150₽ |
|
|
17901 |
Вычислить несобственный интеграл, используя вычеты: $$\int\limits_{0}^{+\infty} \frac{\cos{x}}{(x^2+1)^2}dx$$
|
Теория функций комплексного переменного |
|
|
150₽ |
|
|
12150 |
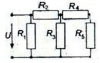
САМОСТОЯТЕЛЬНАЯ РАБОТА 1
Вариант 96.
Расчёт разветвлённой электрической цепи постоянного тока
Для данной электрической цепи определить с использованием законов Ома и Кирхгофа
1. Токи в ветвях
2. Мощность, развиваемую источником энергии, и мощность потребителей
3. Составить баланс мощности
| Последняя цифра номера студенческого билета |
U, В |
R1, Ом |
R2, Ом |
R2, Ом |
R4, Ом |
R5, Ом |
| 6 |
50 |
8 |
11 |
9 |
7 |
14 |
|
Электротехника |
96 |
Разветвлённая электрическая цепь постоянного тока |
150₽ |
|
|
10294 |
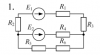
Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии.
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 2, выполнить следующее:
1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений не следует.
2. Определить токи в ветвях методом контурных токов.
3. Определить режимы работы активных элементов и составить баланс мощностей.
Значения ЭДС источников и сопротивлений приемников приведены в табл. 2.
| Предпоследняя цифра учебного шифра студента |
E1, В |
E2, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 2 |
70 |
190 |
17 |
12 |
8 |
13 |
17 |
10 |
|
Электротехника |
221 |
МИИТ. Общая электротехника и электроника. 2016 год |
150₽ |
|





















