Если найти нужную задачу не удаётся, Вы можете оформить Заказ.
Как использовать поиск
| Номер | Условие задачи | Предмет | Задачник | Цена | ||
|---|---|---|---|---|---|---|
| 5281 |
Доказать тождество на основании основных тождеств: $$(A \cap B) \cup C = (A \cup C) \cap (B \cap C)$$ |
Математическая логика | 5₽ | |||
| 5282 |
Доказать тождество на основании основных тождеств: $$(A \cup B) \cap C = (A \cap C) \cup (B \cap C)$$ |
Математическая логика | 5₽ | |||
| 5283 |
Составить таблицу истинности для функции $$f(x_1;x_2 )=(\overline{x_1}\to (x_1 \cap x_2 ))\cup \overline{(\overline{x_1}\cap x_2)}$$ |
Математическая логика | 5₽ | |||
| 5284 |
Составить таблицу истинности для функции $$f(x_1;x_2 )=(\overline{x_2}\to (x_1\cup \overline{x_2} ))\to (\overline{x_1}\cap x_2)$$ |
Математическая логика | 5₽ | |||
| 14342 |
С помощью равносильных преобразований упростить формулу: $$((A\land B)\leftrightarrow B)\leftrightarrow(B\rightarrow A)$$ |
Математическая логика | 100₽ | |||
| 14344 |
Проверить, является ли формула тавтологией с помощью равносильных преобразований. Ответ проверить с помощью таблицы истинности: $$(P\rightarrow Q)\rightarrow((P\rightarrow(Q\rightarrow R))\rightarrow(P\rightarrow R))$$ |
Математическая логика | 100₽ | |||
| 14346 |
Проверить, справедливо ли следующее логическое следование: $$(P\vee\bar{R})\rightarrow Q\ \models\ (P\rightarrow Q)\land R$$ |
Математическая логика | 100₽ | |||
| 15864 |
Упростить выражение: $$\overline{(A\backslash (B \vee C))} \land (\overline{((\bar{A} \vee B) \backslash (A \vee C))} \vee (B\backslash C))$$ |
Математическая логика | 100₽ | |||
| 15918 |
Дано универсальное множество U и три его подмножества A, B и C. Известно, что $|U|=17$, $|\bar{A}|=9$, $|\bar{B}|=5$, $|\bar{C}|=6$, $|\bar{A}\cap\bar{B}|=4$, $|\bar{A}\cap\bar{C}|=3$, $|\bar{B}\cap\bar{C}|=1$, $|\bar{A}\cap\bar{B}\cap\bar{C}|=1$. Найти $|\bar{B}\cap C|$, $|\bar{A}\cap B|$, $|A\cap\bar{B}\cap\bar{C}|$, $|\bar{A}\cap\bar{B}\cap C|$, $|A\cap B\cap C|$. |
Математическая логика | 100₽ | |||
| 16496 |
Пусть A, B, C являются подмножествами некоторого универсального множества E. С помощью диаграмм Эйлера покажите, что выполняются соотношения: |
Математическая логика | 75₽ | |||
| 16498 |
Симметрической разностью множеств A и B (обозначение $A\Delta B$) называют $\left(A\backslash B\right)\cup \left(B\backslash A\right)$. |
Математическая логика | 50₽ | |||
| 16500 |
Упростите выражения, а затем ответьте на вопрос: |
Математическая логика | 75₽ | |||
| 16504 |
14 школьников участвовало в олимпиаде по истории, 16 – в олимпиаде по географии, 10 – в олимпиаде по физике. 8 учеников участвовали в олимпиадах и по истории, и по географии, 4 – в олимпиадах и по истории, и по физике, 9 – в олимпиадах и по географии, и по физике. Во всех трёх олимпиадах участвовали 3 человека. Сколько всего было школьников? |
Математическая логика | 30₽ | |||
| 16710 |
Для данной формулы $\alpha$ алгебры логики записать таблицу истинности. $$\alpha=\left[(\bar{A}\vee \bar{C}) \& \bar{B}\right] \vee \left[ (\bar{A} \to B) \sim C\right]$$ |
Математическая логика | 30₽ | |||
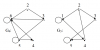
| 16711 | Теория графов | 30₽ | ||||
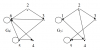
| 16712 | Теория графов | 30₽ | ||||
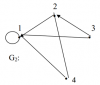
| 16713 | Теория графов | 50₽ | ||||
| 16750 |
Один из школьников: Ваня, Петя, Вася или Игорь случайно разбил в классе стекло. На вопрос, кто это сделал, они дали противоречивые ответы: |
Математическая логика | 50₽ | |||
| 16809 |
Являются ли высказываниями следующие утверждения? Если да, установите, истинны они или ложны: |
Математическая логика | 30₽ | |||
| 16828 |
Возможно ли, что m(A) = 9, m(B) = 16, m(C) = 17 и m(A∩B) = 5, m(A∩C) = 8, m(B∩C) = 13, m(A∪B∪C) = 22 |
Математическая логика | 50₽ | |||
| 16829 |
Докажите, что следующие множества равномощны: [3;7) и [3;7] |
Математическая логика | 150₽ | |||
| 16830 |
С помощью рассуждений докажите, что |
Математическая логика | 150₽ | |||
| 16832 |
Учащиеся 9-х классов пошли в лес за грибами. 80% собирали белые грибы, 70% – моховики, 85% – маслята, 75% – рыжики. Сколько процентов учащихся собирали вместе белые грибы, моховики, маслята и рыжики? |
Математическая логика | 100₽ | |||
| 16833 |
У каждого из тридцати девятиклассников есть одна ручка, один карандаш и одна линейка. После их участия в олимпиаде оказалось, что 26 учеников потеряли ручку, 23 – линейку и 21 – карандаш. Найдите наименьшее возможное количество девятиклассников, потерявших все три предмета. |
Математическая логика | 100₽ |