Если найти нужную задачу не удаётся, Вы можете оформить Заказ.
Как использовать поиск
| Номер | Условие задачи | Предмет | Задачник | Цена | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16420 |
|
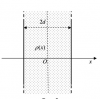
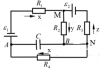
Электростатика | 4-3-10 | ТГУ. Физика | 200₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16422 |
Сколькими способами в таблицу 7×7 можно расставить цифры (от 0 до 9) так, чтобы сумма цифр в каждом квадрате 2×2 не превышала 12, а сумма всех цифр в таблице была максимально возможной? |
МАТЕМАТИКА | 100₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
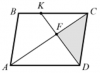
| 16424 | Геометрия | 75₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16426 | Комбинаторика | 150₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16428 |
Вычислить несобственный интеграл или установить его расходимость $$\int_1^{\frac32}\frac{dx}{\sqrt{9-4x^2}}$$ |
Несобственный интеграл | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16430 |
Вычислить интеграл по формуле Ньютона-Лейбница $$\int_0^1\frac{5x^2}{(x^3+8)^2}dx$$ |
Определенный интеграл | 30₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16432 |
В цилиндре под поршнем находится жидкость и ее насыщенный пар. При изотермическом расширении объем пара увеличился в 8,4 раза, а давление уменьшилось в 2,1 раза. Найти отношение массы жидкости к массе пара до расширения. |
Молекулярная физика и термодинамика | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16434 |
На горизонтальной поверхности находится брусок. Коэффициент трения между бруском и поверхностью 0,2. Если к бруску приложить силу F, направленную вверх под углом 30° к горизонту, то брусок будет двигаться по столу равномерно и прямолинейно. Найти ускорение бруска, если к нему приложить в том же направлении силу 1,3F. Принять g = 10 м/с2. |
Механика | 75₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16436 |
|
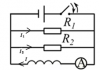
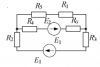
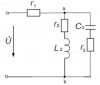
Электродинамика | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16438 |
Груз, подвешенный на упругой пружине, колеблется вдоль вертикали с амплитудой 2 см и периодом 0,5 с. Груз находится на расстоянии 50 см от тонкой собирающей линзы с фокусным расстоянием 20 см. Колебания происходят вблизи горизонтальной главной оптической оси линзы. Масса пружины намного меньше массы груза. Найти максимальную скорость изображения груза на экране. Ответ выразить в сантиметрах в секунду (см/с). |
Оптика | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16440 |
|
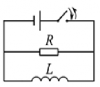
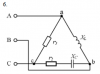
Электродинамика | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16442 |
Расстояние между штрихами дифракционной решетки 4 мкм. На решетку падает нормально свет с длиной волны 0,58 мкм. Максимум какого наибольшего порядка дает эта решетка? |
Оптика | 30₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16444 |
В однозарядном ноне гелия электрон перешел с третьего энергетического уровня на первый. Определить длину волны λ излучения, испущенного ионом гелия. |
Электродинамика | 30₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16446 |
Электрон находится в бесконечно-глубоком одномерном прямоугольном потенциальном ящике шириной L= 0,1 нм. Определить в электронвольтах наименьшую разность энергетических уровней электрона. |
Электродинамика | 30₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16448 |
Активность A некоторого изотопа за время t = 10 сут уменьшилась на 20%. Определить период полураспада T1/2 этого изотопа. |
Электродинамика | 30₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16450 |
Определить длины волн де Бройля α-частицы и протона, прошедших одинаковую ускоряющую разность потенциалов U = 1 кВ. |
Электродинамика | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16452 |
Определять температуру и энергетическую светимость (излучательноегь) абсолютно черного тела, если максимум энергии излучения приходится на длину волны 600 нм. |
Электродинамика | 40₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16454 |
Во сколько раз энергия заряда Q, распределенного равномерно по поверхности шара с радиусом R, больше (или меньше) энергии этого заряда равномерно распределенного по объёму шара того же радиуса? |
Электродинамика | 100₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16456 |
Электрическое поле образовано двумя неподвижными, вертикально расположенными, параллельными, разноимённо заряженными непроводящими пластинами. Пластины расположены на расстоянии 5 см друг от друга. Напряжённость поля между пластинами 104 В/м. Между пластинами на равном расстоянии от них помещён шарик с зарядом 10-5 Кл и массой 10 г. После того как шарик отпустили, он начинает падать. Какую скорость будет иметь шарик, когда коснётся одной 13 пластин? |
Электродинамика | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16458 | Электродинамика | 150₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16460 | Электромагнетизм | 150₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16462 |
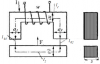
Проходная характеристика при UCU = 5 В
Выходная характеристика при Uэм = 0,5 В
|
Постоянный ток | 100₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16464 |
Положительно заряженная частица с зарядом q и массой m влетает в однородное электрическое ноле с напряжённостью Е так, что вектор начальной скорости совпадает по направлению с вектором напряжённости электрического поля. За время t скорость частицы увеличивается от начальной скорости v0 до скорости v. Определите значение величины, обозначенной «?».
|
Электродинамика | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16468 |
Электрический заряд q, находясь в точке электрического поля с потенциалом φ, обладает потенциальной энергией W. Определите значения величин, обозначенных «?». Во сколько раз изменится потенциал данной точки электрического поля при увеличении заряда q в α раз?
|
Электродинамика | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16472 |
Частица с зарядом q и массой m, начиная движение из состояния покоя в однородном электрическом поле с напряжённостью Е, приобретает скорость пройдя расстояние d. При этом напряжение, ускоряющее частицу, составляет U. Определите значения величин, обозначенных «?».
|
Электродинамика | 40₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16474 |
|
Электродинамика | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16476 |
Лабораторная работа №1. Исследование свойств полупроводниковых диодов Прямое включение
Обратное включение
|
Постоянный ток | 100₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16478 |
Число N обладает таким свойством: если в нём вычеркнуть несколько цифр (одну или больше, но чтобы что-то осталось), то всегда получается простое число или 1. Какое наибольшее число знаков может иметь N? |
Комбинаторика | 100₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16480 |
При плоском движении частицы в некоторый момент времени, когда величина скорости равна v = 106 м/с, вектор ускорения по величине равен a = 104 м/с2 и образует угол α = 30° с вектором скорости. Вычислите приращение ∆v модуля скорости частицы за последующие ∆t = 0,02 с. С какой угловой скоростью ω вращается вектор скорости? На какой угол ∆φ повернется вектор скорости частицы за последующие ∆t = 0,02 с? Каков радиус R кривизны траектории в малой окрестности рассматриваемой точки? |
Механика | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16482 |
Допустим, что на планете Фантазия реализован следующий эксперимент. Груз на нити длиной l = 3 м отклоняют на некоторый угол α и отпускают. Далее в процессе колебаний максимальная сила натяжения отличается от минимальной в k = 4 раза. Такой же угол α с вертикалью образует эта же нить маятника, если груз обращается с периодом T = 4 с вокруг вертикальной оси, проходящей через точку подвеса. Определите ускорение свободного падения на планете. Считайте планету однородным шаром. |
Механика | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16484 |
В нижней точке жесткого проволочного шероховатого кольца радиуса R = 2 м, находящегося в вертикальной плоскости, покоится бусинка. Кольцо очень медленно раскручивают вокруг вертикальной оси, касающейся кольца. Найдите коэффициент μ трения скольжения бусинки по кольцу, если при угловой скорости ω = 3,2 с-1 бусинка поднялась на высоту, равную половине радиуса R/2. При каких значениях величины ω2R/g задача не имеет решения? |
Механика | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16486 |
Бусинка массы m надета на гладкое проволочное кольцо радиуса R = 2 м, плоскость которого наклонена под углом α = 30° к горизонту. Кольцо жесткое и закреплено неподвижно. В некоторый момент бусинка начинает движение из верхней точки кольца с пренебрежимо малой скоростью. Найдите ускорение a бусинки в нижней точке кольца (укажите величину и направление). С какой по величине силой N действует кольцо на бусинку в момент прохождения нижней точки кольца. Какой угол β образует сила N с вертикалью? |
Механика | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16488 |
На горизонтальной поверхности лежит гладкий полушар массой M = 200 г. Из его верхней точки в противоположных направлениях с пренебрежимо малыми начальными скоростями скользят две шайбы с массами m1 = 20 г и m2 = 15 г. Из-за трения между полушаром и горизонтальной поверхностью движение полушара начинается в тот момент, когда одна из шайб пройдет Δ = 1/36 длины окружности большого круга. Вычислите коэффициент μ трения скольжения полушара по поверхности. Шайбы приходят в движение одновременно. |
Механика | 200₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16490 | Геометрия | 50₽ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16494 |
Какое наибольшее количество узлов клетчатого листа можно отметить так, чтобы никакие три отмеченные точки не лежали на одной прямой и точка пересечения медиан любого треугольника с вершинами в отмеченных узлах не являлась узлом? |
МАТЕМАТИКА | 200₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16496 |
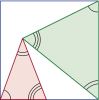
Пусть A, B, C являются подмножествами некоторого универсального множества E. С помощью диаграмм Эйлера покажите, что выполняются соотношения: |
Математическая логика | 75₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16498 |
Симметрической разностью множеств A и B (обозначение $A\Delta B$) называют $\left(A\backslash B\right)\cup \left(B\backslash A\right)$. |
Математическая логика | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16500 |
Упростите выражения, а затем ответьте на вопрос: |
Математическая логика | 75₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16502 |
Трамвай движется с постоянным тангенциальным ускорением по круговому повороту, который является четвертью окружности радиуса R. В начале поворота величина скорости трамвая равна v0. Тангенциальная составляющая ускорения вдвое больше начальной нормальной. Найдите отношение нормальной и тангенциальной составляющих ускорения при завершении поворота. Если на горизонтальном полу трамвая стоит коробка, то при каких значения коэффициента трения скольжения она не будет скользить по полу? |
Механика | 100₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16504 |
14 школьников участвовало в олимпиаде по истории, 16 – в олимпиаде по географии, 10 – в олимпиаде по физике. 8 учеников участвовали в олимпиадах и по истории, и по географии, 4 – в олимпиадах и по истории, и по физике, 9 – в олимпиадах и по географии, и по физике. Во всех трёх олимпиадах участвовали 3 человека. Сколько всего было школьников? |
Математическая логика | 30₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16506 |
|
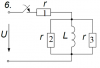
Электротехника | 1-0-6 | СамГУПС Саратов. Общая электротехника и электроника. 2018 год | 100₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16508 |
|
Электротехника | 2-0-6 | СамГУПС Саратов. Общая электротехника и электроника. 2018 год | 300₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16510 |
|
Электротехника | 3-0-6 | СамГУПС Саратов. Общая электротехника и электроника. 2018 год | 300₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16512 |
|
Электротехника | 4-0-6 | СамГУПС Саратов. Общая электротехника и электроника. 2018 год | 300₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16514 |
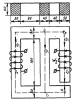
Размеры магнитопровода на рис. 5 даны в мм. Магнитопровод выполнен из электротехнической стали, кривая намагничивания которой представлена в табл. 2. Величины токов и число витков обмотки для каждого варианта даны в табл. 3.
|
Электротехника | 5-0-6 | СамГУПС Саратов. Общая электротехника и электроника. 2018 год | 300₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16516 |
Расчет выпрямителя источника электропитания электронного устройства
Требуется: |
Электротехника | 6-0-6 | СамГУПС Саратов. Общая электротехника и электроника. 2018 год | 100₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16520 |
Интенсивность света двух различных длин волн λ1 и λ2 измеряется в жидкости непосредственно у поверхности и на глубине 2 м. Оказалось, что I01 = I02 начальная интенсивность (на поверхности) одинакова, а на глубине ld1 = 2∙Id2. Определить. на какой глубине интенсивность света длиной волны λ1 превысит интенсивность света длиной волны λ2 в 10 раз. |
Оптика | 100₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16522 |
Диаметр поршня шприца ветеринарного ШВВ равен 20 мм. Внутренний диаметр иглы 1 мм. Какое давление ветврач должен прикладывать к поршню, чтобы время инъекции составляло 10 с? Длина хода поршня 8 см. Плотность вводимого лекарственного раствора принять равной плотности воды, т.е. 103 кг/м3. |
Биофизика | 021 | ИжГСХА. Физика с основами биофизики. 2013 год | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16526 |
Рабочее колесо установленного в коровнике вентилятора МЦ вращается так, что зависимость частоты вращения от времени задается уравнением: $\nu=А\sqrt{t}+В$, где А = 0,1 с-3/2 и В = 12 с-1. Сколько оборотов сделает барабан через 2 мин от начала вращения? |
Биофизика | 001 | ИжГСХА. Физика с основами биофизики. 2013 год | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16528 |
Вычислить момент инерции руки человека относительно плечевого сустава. Масса руки 4,1 кг, ее длина (при пальцах, сжатых в кулак) 0,56 м. Для упрощения принять руку за однородный стержень. С каким ускорением начнет перемещаться рука из горизонтального положения в вертикальное под действием собственной тяжести? Центр масс руки расположен на расстоянии 28 см от плечевого сустава |
Биофизика | 002 | ИжГСХА. Физика с основами биофизики. 2013 год | 50₽ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||