Если найти нужную задачу не удаётся, Вы можете оформить Заказ.
Как использовать поиск
| Номер | Условие задачи | Предмет | Задачник |
Цена |
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 14854 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-19 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | |||||||||||||||
| 18260 |
Найти экстремаль функционалов со старшей производной $$J[y]=\int_0^{\pi}({y''}^2-2{y'}^2-16y\sin x)dx,$$ удовлетворяющие граничным условиям $y(0)=0,\ y'(0)=0,\ y(\pi)=0,\ y'(\pi)=\pi^2$. |
Вариационное исчисление | 200₽ | |||||||||||||||||
| 13720 |
Идеальный газ находится в однородном поле тяжести Земли. Молярная масса газа М = 29∙10-3 кг/моль. Абсолютная температура газа меняется с высотой h по закону T(h) = T0(l + a∙h). Найти давление газа p на высоте h. На высоте h = 0 давление газа p0 = 105 Па.
|
ФИЗИКА | 6-2-19 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 16701 |
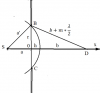
Точки K и L лежат на боковых сторонах AB и CD трапеции ABCD соответственно, причём площадь четырёхугольника BCLK в 5 раз меньше площади четырёхугольника ADLK; CL = 3, DL = 15, CK = 4, KL⊥AB. Найдите DK. |
Геометрия | 200₽ | |||||||||||||||||
| 11776 |
Используя необходимые и достаточные условия экстремума функционала, исследовать функционал $J(y)$. Если функционал имеет слабый или сильный экстремум, то вычислить экстремальное значение $J^*$. |
Вариационное исчисление | 3.23 | Вариационное исчисление | 200₽ | |||||||||||||||
| 14934 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-55 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | |||||||||||||||
| 13018 |
Задан закон движения $\vec r(t)$ материальной точки в координатной плоскости $XY$ в интервале времени от $t_1$ до $t_2$. Найти уравнение траектории $y=y(x)$ и построить график. Найти модуль вектора перемещения точки в заданном интервале времени. Найти модули начальной $v_1$ и $v_2$ конечной скоростей точки.
|
ФИЗИКА | 1-1-12 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 16741 |
Сферический конденсатор заряжен зарядом q, а его обкладки имеют радиусы r и R, причём r < R. Определите напряжённость электрического поля внутри конденсатора на расстоянии x от его центра. Вычислите плотности энергии поля внутри конденсатора вблизи каждой из обкладок. Сравните их с величиной W/V, где W - полная энергия конденсатора, а V - объём пространства между обкладками. |
Электростатика | 200₽ | |||||||||||||||||
| 15014 | Оптика | 200₽ | ||||||||||||||||||
| 13100 |
Частица движется по окружности радиуса R. Угол поворота радиус-вектора частицы меняется со временем по закону φ(t) . Найти число оборотов N, которые частица совершит в интервале времени от t1 до t2. Найти модули векторов тангенциального aτ, нормального an и полного a ускорений, а также угол α между векторами тангенциального и полного ускорений в момент времени t2.
|
ФИЗИКА | 1-3-12 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 4400 |
Посередине откачанной и запаянной с обоих концов горизонтальной трубки длинной L = 1 м находится столбик ртути длиной Н = 20 см. Если трубку поставить вертикально, столбик ртути сместится на Δl = 10 см. До какого давления p была откачана трубка? Плотность ртути ρ0 = 13,6 г/м3. Ответ дать в кПа. |
Молекулярная физика и термодинамика | 200₽ | |||||||||||||||||
| 13576 |
Идеальный газ - азот совершает замкнутый цикл, состоящий из трех процессов 1-2, 2-3 и 3-1, идущий по часовой стрелке. Значения давления и объема газа в состояниях 1, 2 и 3 равны соответственно p1, V1, p2, V2 и p3, V3. Найти термический к.п.д. цикла.
|
ФИЗИКА | 5-2-7 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 14870 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-27 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | |||||||||||||||
| 13736 |
Пространство между двумя параллельными пластинами площадью S = 300 см2 заполнено газом. Пластины находятся друг от друга на расстоянии h = 5 мм. Одна пластина поддерживается при температуре Т1, другая - при температуре Т2. Найти количество теплоты Q прошедшее посредством теплопроводности от одной пластины к другой за время t = 10 мин. Газ находится при нормальных условиях. Эффективный диаметр молекул газа равен d = 0,36 нм. Показатель адиабаты газа γ.
|
ФИЗИКА | 6-3-7 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 14950 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-60 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | |||||||||||||||
| 13034 |
Задан закон движения $\vec r(t)$ материальной точки в координатной плоскости $XY$ в интервале времени от $t_1$ до $t_2$. Найти уравнение траектории $y=y(x)$ и построить график. Найти модуль вектора перемещения точки в заданном интервале времени. Найти модули начальной $v_1$ и $v_2$ конечной скоростей точки.
|
ФИЗИКА | 1-1-20 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
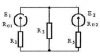
| 11880 |
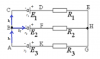
|
Постоянный ток | 200₽ | |||||||||||||||||
| 13116 |
Частица движется по окружности радиуса R. Угол поворота радиус-вектора частицы меняется со временем по закону φ(t) . Найти число оборотов N, которые частица совершит в интервале времени от t1 до t2. Найти модули векторов тангенциального aτ, нормального an и полного a ускорений, а также угол α между векторами тангенциального и полного ускорений в момент времени t2.
|
ФИЗИКА | 1-3-20 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 4408 |
Найти удельные теплоемкости сV и сP некоторого двухатомного газа, если плотность его при нормальных условиях составляет 1,43 кг/м3. |
Молекулярная физика и термодинамика | 200₽ | |||||||||||||||||
| 8400 |
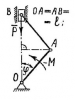
ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ |
Теоретическая механика | Д3.14 | Теоретическая механика 2 | 200₽ | |||||||||||||||
| 13592 |
Идеальный газ - азот совершает замкнутый цикл, состоящий из трех процессов 1-2, 2-3 и 3-1, идущий по часовой стрелке. Значения давления и объема газа в состояниях 1, 2 и 3 равны соответственно p1, V1, p2, V2 и p3, V3. Найти термический к.п.д. цикла.
|
ФИЗИКА | 5-2-15 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 14886 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-31,91 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | |||||||||||||||
| 13752 |
Пространство между двумя параллельными пластинами площадью S = 300 см2 заполнено газом. Пластины находятся друг от друга на расстоянии h = 5 мм. Одна пластина поддерживается при температуре Т1, другая - при температуре Т2. Найти количество теплоты Q прошедшее посредством теплопроводности от одной пластины к другой за время t = 10 мин. Газ находится при нормальных условиях. Эффективный диаметр молекул газа равен d = 0,36 нм. Показатель адиабаты газа γ.
|
ФИЗИКА | 6-3-15 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 14966 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-68 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | |||||||||||||||
| 9012 | Теоретическая механика | C3.18. | Теоретическая механика | 200₽ | ||||||||||||||||
| 15046 |
Уединённая металлическая сфера электроёмкостью 40 пФ заряжена до потенциала 3 кВ. Определить энергию электрического поля, заключённого в сферическом слое, ограниченном сферой и концентрической с ней сферической поверхностью, радиус которой в два раза больше радиуса сферы. |
Электростатика | 200₽ | |||||||||||||||||
| 13452 |
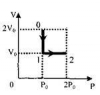
Один моль идеального газа переходит из начального состояния 1 в конечное состояние 3 в результате двух изопроцессов 1-2 и 2-3. Значения давления и объема газа в состояниях 1 и 3 равны соответственно p1, V1 и p3, V3. Найти давление, объем и температуру газа p2, V2, T2 в промежуточном состоянии 2. Изобразить процессы в координатах p-V, p-T и V-T.
|
ФИЗИКА | 4-2-5 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 5044 | Теоретическая механика | D2.8 | Теоретическая механика | 200₽ | ||||||||||||||||
| 8760 |
|
Электромагнетизм | 200₽ | |||||||||||||||||
| 8140 |
|
Электротехника | 200₽ | |||||||||||||||||
| 14514 |
Космический объект с массой покоя m0 движется со скоростью V имея импульс Р и кинетическую энергию Т. Собственная длина объекта в направлении движения l0, релятивистское изменение этой длины Δl. Определить параметры, обозначенные для Вашего варианта знаком “?"
|
Специальная теория относительности | 7-4 | ЗабГУ. Физика. 2011 год | 200₽ | |||||||||||||||
| 13468 |
Один моль идеального газа переходит из начального состояния 1 в конечное состояние 3 в результате двух изопроцессов 1-2 и 2-3. Значения давления и объема газа в состояниях 1 и 3 равны соответственно p1, V1 и p3, V3. Найти давление, объем и температуру газа p2, V2, T2 в промежуточном состоянии 2. Изобразить процессы в координатах p-V, p-T и V-T.
|
ФИЗИКА | 4-2-13 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 8656 |
ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ МАТЕРИАЛЬНОЙ ТОЧКИ |
Теоретическая механика | Д1.1 | Теоретическая механика 2 | 200₽ | |||||||||||||||
| 12758 |
Материальная точка движется по окружности радиуса R так, что зависимость угла поворота φ от времени $\varphi =a+bt+ct^2$. Определить для момента времени t1 c линейную и угловую скорости точки; нормальное, тангенциальное и полное ускорения точки, а для промежутка времени t1 c до t2 c перемещение точки и пройденный путь.
|
Механика | 2-9 | ЗабГУ. Физика. 2011 год | 200₽ | |||||||||||||||
| 16808 |
a) Нарисуйте на клетчатой бумаге выпуклый шестиугольник, вершины которого лежат в вершинах клеток, а стороны идут не обязательно по сторонам клеток, который можно двумя прямыми разрезать на четыре равные части. |
МАТЕМАТИКА | 200₽ | |||||||||||||||||
| 16850 |
Все рёбра правильной пирамиды SABCD с вершиной S равны 2. Плоскость, параллельная прямым AC и SB, пересекает рёбра AB и BC в точках M и N. Найдите периметр сечения пирамиды этой плоскостью, если $MN=\sqrt{2}$. |
Стереометрия | 200₽ | |||||||||||||||||
| 12774 |
Материальная точка движется по окружности радиуса R так, что зависимость угла поворота φ от времени $\varphi =a+bt+ct^2$. Определить для момента времени t1 c линейную и угловую скорости точки; нормальное, тангенциальное и полное ускорения точки, а для промежутка времени t1 c до t2 c перемещение точки и пройденный путь.
|
Механика | 2-17 | ЗабГУ. Физика. 2011 год | 200₽ | |||||||||||||||
| 15902 | Электротехника | 200₽ | ||||||||||||||||||
| 14776 | Теоретическая механика | С1-1 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | ||||||||||||||||
| 8894 |
Используя необходимые и достаточные условия экстремума функционала, исследовать функционал $J(y)$. Если функционал имеет слабый или сильный экстремум, то вычислить экстремальное значение $J^*$. $$J[y]=\int_{0}^{2}\frac{1}{y'}dx;\ y(0)=0,\ y(2)=5$$ |
Вариационное исчисление | 3.8 | Вариационное исчисление | 200₽ | |||||||||||||||
| 4362 |
Два сосуда одинаковой емкости содержат кислород. В одном сосуде давление p1 = 1 МПа и температура T1 = 400 К, в другом p2 = 1,5 МПа, T2 = 250 К. Сосуды соединили трубкой и охладили находящийся в них кислород до температуры T = 300 К. |
Молекулярная физика и термодинамика | 200₽ | |||||||||||||||||
| 16548 |
Идеальный газ совершает цикл, состоящий из изохоры, адиабаты и изотермы, при этом изотермический процесс происходит при минимальной температуре цикла. Изобразите график цикла и найдите его КПД. Максимальная температура в цикле в 4 раза больше минимальной. |
Молекулярная физика и термодинамика | 200₽ | |||||||||||||||||
| 12790 |
Материальная точка движется по окружности радиуса R так, что зависимость угла поворота φ от времени $\varphi =a+bt+ct^2$. Определить для момента времени t1 c линейную и угловую скорости точки; нормальное, тангенциальное и полное ускорения точки, а для промежутка времени t1 c до t2 c перемещение точки и пройденный путь.
|
Механика | 2-25 | ЗабГУ. Физика. 2011 год | 200₽ | |||||||||||||||
| 14792 | Теоретическая механика | С1-9 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | ||||||||||||||||
| 4370 |
|
Молекулярная физика и термодинамика | 200₽ | |||||||||||||||||
| 8714 | Теоретическая механика | Д8.11 | Теоретическая механика 2 | 200₽ | ||||||||||||||||
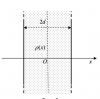
| 16414 |
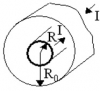
|
Электростатика | 4-3-6 | ТГУ. Физика | 200₽ | |||||||||||||||
| 14816 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-00 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | |||||||||||||||
| 9658 |
Даны вершины $A_1(1,4,-2),А_2(-3,0,3), А_3(8,0,1), А_4(1,-4,3)$. Построить пирамиду в декартовой ортонормированной системе координат. Найти: |
Аналитическая геометрия | 200₽ | |||||||||||||||||
| 16681 |
В цилиндре под поршнем находится влажный воздух при температуре 100°С. Парциальное давление водяного пара 25кПа. В медленном изотермическом процессе объём уменьшается в 5 раз. Найдите парциальное давление водяного пара после окончания процесса. Нарисуйте график этого процесса в координатах p,V. |
Молекулярная физика и термодинамика | 200₽ |