Если найти нужную задачу не удаётся, Вы можете оформить Заказ.
Как использовать поиск
| Номер | Условие задачи | Предмет | Задачник | Цена | ||
|---|---|---|---|---|---|---|
| 15366 |
|
Механика | 1.3.31 | Физика. Решение сложных задач | 50₽ | |
| 15368 |
На дне бассейна лежит тонкий цилиндрический стержень длиной L = 1 м, состоящий из двух половин с одинаковыми площадями поперечного сечения и плотностями ρ1 = 0,5 г/см и ρ2 = 2,0 г/см3. В бассейн медленно наливают воду плотностью ρ0 = 1,0 г/см3. При какой глубине h воды в бассейне стержень будет составлять с поверхностью воды угол α = 45°? |
Механика | 1.3.32 | Физика. Решение сложных задач | 50₽ | |
| 15370 |
|
Механика | 1.3.33 | Физика. Решение сложных задач | 50₽ | |
| 15372 |
|
Механика | 1.3.34 | Физика. Решение сложных задач | 50₽ | |
| 15374 |
|
Механика | 1.4.1 | Физика. Решение сложных задач | 50₽ | |
| 15376 |
Граната массой m = 1 кг разорвалась на высоте h = 6 м над землей на два осколка. Непосредственно перед разрывом скорость гранаты была направлена горизонтально и по модулю равна v = 10 м/с. Один из осколков массой m1 =0,4 кг полетел вертикально вниз и упал на землю под местом разрыва со скоростью v1 = 40 м/с. Чему равен модуль скорости v2 второго осколка сразу после разрыва? Ускорение свободного падения g = 10 м/с2, влиянием воздуха пренебречь |
Механика | 1.4.2 | Физика. Решение сложных задач | 50₽ | |
| 15378 |
Кузнечик сидит на одном из концов соломинки длиной l = 50 см, покоящейся на гладком полу. С какой минимальной относительно пола скоростью v0 он должен прыгнуть, чтобы при приземлении попасть точно на второй конец соломинки? Масса кузнечика в β = 3 раза больше массы соломинки. Размерами кузнечика и трением между полом и соломинкой пренебречь. Ускорение свободного падения g = 10 м/с2. |
Механика | 1.4.3 | Физика. Решение сложных задач | 50₽ | |
| 15380 | Механика | 1.4.4 | Физика. Решение сложных задач | 50₽ | ||
| 15382 |
|
Механика | 1.4.5 | Физика. Решение сложных задач | 50₽ | |
| 15384 |
Камень массой m = 0,1 кг бросают горизонтально с вершины холма, склон которого составляет угол α = 30° с горизонтом. Определить, какая работа A была совершена при броске, если камень упал на склон на расстоянии l = 40 м от вершины. Считать, что бросок выполнен непосредственно от поверхности земли. Ускорение свободного падения принять равным g = 10 м/c2. Сопротивлением воздуха пренебречь |
Механика | 1.4.6 | Физика. Решение сложных задач | 50₽ | |
| 15386 |
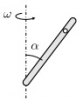
Шарик массой m = 100 г подвешен на нити длиной l = 1 м. Его приводят в движение так, что он вращается по окружности, лежащей в горизонтальной плоскости, которая находится на расстоянии l/2 от точки подвеса. Какую работуA нужно совершить для реализации такого движения? Ускорение свободного падения принять равным g = 10 м/c2. |
Механика | 1.4.7 | Физика. Решение сложных задач | 50₽ | |
| 15388 |
Шарик массой m = 100 г подвешен на нити длиной l = 1 м. Его приводят в движение так, что он вращается по окружности, лежащей в горизонтальной плоскости, которая находится на расстоянии l/2 от точки подвеса. Какую работуA нужно совершить для реализации такого движения? Ускорение свободного падения принять равным g = 10 м/c2. |
Механика | 1.4.7 | Физика. Решение сложных задач | 50₽ | |
| 15390 |
Развивая максимальную мощность двигателя, автобус движется по горизонтальному участку шоссе с постоянной скоростью v0 = 108 км/ч. Когда автобус при неизменной мощности, развиваемой двигателем, въезжает на подъем с углом наклона α1 = 5°, его скорость падает до v1 = 72 км/ч. С какой скоростью v2 автобус будет преодолевать подъем с углом наклона α2 = 2,5° при той же мощности, развиваемой двигателем? Проскальзывание ведущих колес автобуса на всех участках шоссе отсутствует. Силу сопротивления воздуха считать пропорциональной скорости автобуса. |
Механика | 1.4.8 | Физика. Решение сложных задач | 50₽ | |
| 15392 |
|
Механика | 1.4.9 | Физика. Решение сложных задач | 50₽ | |
| 15394 |
|
Механика | 1.4.10 | Физика. Решение сложных задач | 50₽ | |
| 15396 |
|
Механика | 1.4.11 | Физика. Решение сложных задач | 50₽ | |
| 15398 |
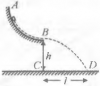
С горки высоты h = 2 м с углом наклона α = 45° начинают скатываться санки с нулевой начальной скоростью. Найти скорость v санок у основания горки, если на верхней половине горки коэффициент трения пренебрежимо мал, а на нижней половине коэффициент трения μ = 0,1. |
Механика | 1.4.12 | Физика. Решение сложных задач | 50₽ | |
| 15400 |
|
Механика | 1.4.13 | Физика. Решение сложных задач | 50₽ | |
| 15402 |
|
Механика | 1.4.14 | Физика. Решение сложных задач | 50₽ | |
| 15404 |
|
Механика | 1.4.15 | Физика. Решение сложных задач | 50₽ | |
| 15406 |
Человек массой M = 70 кг, неподвижно стоявший на коньках, бросил вперед в горизонтальном направлении снежный ком массой m = 3,5 кг. Какую работу A совершил человек при броске, если после броска он откатился назад на расстояние S = 0,2 м? Коэффициент трения коньков о лед μ = 0,01. Ускорение свободного падения принять равным g = 10 м/c2. |
Механика | 1.4.16 | Физика. Решение сложных задач | 50₽ | |
| 15408 |
Лабораторная работа №8 |
Электромагнетизм | 50₽ | |||
| 15410 |
ПРАКТИЧЕСКАЯ РАБОТА N4; |
Электротехника | 100₽ | |||
| 15412 |
ПРАКТИЧЕСКАЯ РАБОТА № 5 |
Электротехника | 100₽ | |||
| 15414 |
Пуля летит горизонтально со скоростью v0 =160 м/с, пробивает стоящую на горизонтальной шероховатой поверхности коробку и продолжает движение в прежнем направлении со скоростью αv0, где α = 1/4. Масса коробки в 12 раз больше массы пули. Коэффициент трения скольжения между коробкой и поверхностью μ = 0,3. На какое расстояние S переместится коробка к моменту, когда ей скорость уменьшится на 20%? |
Механика | 1.4.17 | Физика. Решение сложных задач | 50₽ | |
| 15416 | Механика | 1.4.18 | Физика. Решение сложных задач | 50₽ | ||
| 15418 |
Из пушки производится выстрел таким образом, что дальность полета снаряда в n = 2 раза превышает максимальную высоту траектории. Считая известным модуль начального импульса снаряда р0 = 1000 (кг∙м)/с, определить модуль его импульса p в верхней точке траектории. Сопротивлением воздуха пренебречь |
Механика | 1.4.19 | Физика. Решение сложных задач | 50₽ | |
| 15420 |
Граната, брошенная под углом к горизонту, разрывается в верхней точке траектории на два одинаковых осколка. Один из осколков упал на землю через время t1 = 0,5 с после разрыва гранаты. Через какое время t2 подле разрыва окажется на земле второй осколок, упавший позднее первого, если разрыв гранаты произошел на высоте h = 10 м над поверхностью земли? Сопротивлением воздуха пренебречь. Ускорение свободного падения g = 10 м/c2. |
Механика | 1.4.20 | Физика. Решение сложных задач | 50₽ | |
| 15422 |
На прямолинейном горизонтальном участке пути стоят N = 5 одинаковых вагонов. Промежутки между соседними вагонами одинаковы и равны L = 30 м. К крайнему вагону подкатывается еще один такой же вагон, имеющий скорость v0 = 2 м/c. В результате N последовательных столкновений, и каждом из которых сталкивающиеся вагоны сцепляются вместе, все N + 1 вагонов соединяются в один состав. Найти время τ между первым и последним столкновениями. Силами сопротивления движению вагонов пренебречь. |
Механика | 1.4.21 | Физика. Решение сложных задач | 50₽ | |
| 15424 |
Гиря массой m = 1 кг подвешена на веревке. За свободный конец веревки гирю начинают поднимать вертикально вверх. Какую работу A нужно совершить, чтобы поднять гирю на высоту h = 2 м за время τ = 3 с? Считать, что сила натяжения веревки во время подъема груза постоянна. Веревку считать невесомой и нерастяжимой. Ускорение свободного падения принять равным g = 10 м/c2. |
Механика | 1.4.22 | Физика. Решение сложных задач | 50₽ | |
| 15448 |
|
Механика | 1.4.34 | Физика. Решение сложных задач | 50₽ | |
| 15450 | Механика | 10₽ | ||||
| 15464 |
На гладкой горизонтальной плоскости стоят две одинаковые гладкие горки высотой H = 1 м и массой M = 1 кг каждая. На вершине одной из них находится маленькая шайба массой m = 1 г (см. рисунок). Шайба соскальзывает без начальной скорости в направлении второй горки. Найдите скорости горок после завершения процесса всех столкновений. Ускорение свободного падения g = 10 м/c2. |
Механика | 1.4.41 | Физика. Решение сложных задач | 50₽ | |
| 15468 |
Тележка массой m1 = 0,8 кг движется по инерции со скоростью v0 = 2,5 м/c. На тележку с высоты h = 50 см вертикально падает кусок пластилина массой m2 = 0,2 кг и прилипает к ней. Рассчитайте энергию, которая перешла во внутреннюю при этом ударе. |
Механика | 1.4.43 | Физика. Решение сложных задач | 50₽ | |
| 15470 |
|
Механика | 1.4.46 | Физика. Решение сложных задач | 50₽ | |
| 15472 |
|
Механика | 1.5.1 | Физика. Решение сложных задач | 50₽ | |
| 15474 |
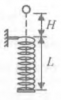
К потолку покоящейся кабины лифта на пружине жесткостью k = 10 Н/м подвешена гиря массой m = 1 кг. В некоторый момент времени лифт начинает движение вверх с постоянным ускорением a = 1 м/c2. Какой путь S пройдет кабина лифта к тому моменту, когда длина пружины первый раз станет максимальной? |
Механика | 1.5.2 | Физика. Решение сложных задач | 50₽ | |
| 15476 |
Груз массой m = 2 кг, закреплённый на пружине жёсткостью k = 200 Н/м, совершает гармонические колебания. Максимальное ускорение груза при этом равно amax = 10 м/c2. Какова максимальная скорость груза? |
Механика | 1.5.3 | Физика. Решение сложных задач | 50₽ | |
| 15478 |
Математический маятник отклонили от положения равновесия на малый угол α0 = 0,1 рад и отпустили без начальной скорости, после чего маятник стал совершать гармонические колебания. Найти максимальную величину vymax вертикальной составляющей скорости маятника. Длина маятника l = 0,4 м. Ускорение свободного падения принять равным g = 10 м/c2. Считать, что sinα = α. |
Механика | 1.5.4 | Физика. Решение сложных задач | 50₽ | |
| 15480 |
Тело массой m = 0,1 кг, надетое на гладкий горизонтальный стержень, связано пружиной жесткостью k = 10 Н/м с неподвижной стенкой. Тело смещают от положения равновесия на расстояние x0 = 10 см и отпускают без начальной скорости. Найти среднюю скорость тела vср за время, в течение которого оно проходит из крайнего положения путь x0/2. |
Механика | 1.5.5 | Физика. Решение сложных задач | 50₽ | |
| 15482 |
Смещение груза пружинного маятника меняется с течением времени по закону $$x = A\sin\frac{2\pi t}{T},$$ |
Механика | 1.5.6 | Физика. Решение сложных задач | 50₽ | |
| 15484 |
|
Механика | 1.5.7 | Физика. Решение сложных задач | 50₽ | |
| 15486 |
|
Механика | 1.5.8 | Физика. Решение сложных задач | 50₽ | |
| 15488 |
Груз массой M = 1 кг подвешен на пружине. Удерживая груз в положении равновесия, на него кладут брусок массой m = 0,1 кг, а затем отпускают. С какой максимальной силой брусок будет действовать на груз в процессе движения? Ускорение свободного падения g = 10 м/c2. Сопротивлением воздуха пренебречь. |
Механика | 1.5.9 | Физика. Решение сложных задач | 50₽ | |
| 15490 |
|
Механика | 1.5.10 | Физика. Решение сложных задач | 50₽ | |
| 15492 |
|
Механика | 1.5.11 | Физика. Решение сложных задач | 50₽ | |
| 15494 | Механика | 1.5.12 | Физика. Решение сложных задач | 50₽ | ||
| 15496 |
Горизонтальная доска совершает гармонические колебания в горизонтальном направлении с периодом T = 2 c. При какой амплитуде колебаний A, лежащее на ней тело начнет скользить? Коэффициент трения между доской и телом μ = 0,2, ускорение свободного падения g = 10 м/c2. |
Механика | 1.5.13 | Физика. Решение сложных задач | 50₽ | |
| 15498 |
|
Механика | 1.5.14 | Физика. Решение сложных задач | 50₽ | |
| 15500 |
Школьник бросил камень с начальной скоростью v0 = 20 м/c под углом α = 45° к горизонту перпендикулярно берегу озера со спокойной водой. Камень упал в воду, и через время T = 136 c после момента броска к берегу начали приходить волны. Школьник подсчитал, что за промежуток времени τ = 10 c о берег ударяется n = 30 волн. Пренебрегая влиянием воздуха на движение камня, найти длину волны на поверхности воды. Считать, что бросок камня производится практически от уровня воды. Ускорение свободного падения принять равным g = 10 м/c2. |
Механика | 1.5.15 | Физика. Решение сложных задач | 50₽ |