Если найти нужную задачу не удаётся, Вы можете оформить Заказ.
Как использовать поиск
| Номер | Условие задачи | Предмет | Задачник |
Цена |
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16541 |
За круглым столом сидят 25 рыцарей, которые представляют два ордена. В зале тусклый свет, поэтому каждый видит только четырёх ближайших соседей – по два слева и справа. Докажите, что один из рыцарей видит слева и справа поровну рыцарей своего ордена. |
МАТЕМАТИКА | 200₽ | |||||||||||||||||
| 8676 |
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ |
Теоретическая механика | Д3.13 | Теоретическая механика 2 | 200₽ | |||||||||||||||
| 12776 |
Материальная точка движется по окружности радиуса R так, что зависимость угла поворота φ от времени $\varphi =a+bt+ct^2$. Определить для момента времени t1 c линейную и угловую скорости точки; нормальное, тангенциальное и полное ускорения точки, а для промежутка времени t1 c до t2 c перемещение точки и пройденный путь.
|
Механика | 2-18 | ЗабГУ. Физика. 2011 год | 200₽ | |||||||||||||||
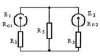
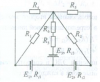
| 15904 | Электротехника | 200₽ | ||||||||||||||||||
| 5047 |
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ |
Теоретическая механика | Д3.8 | Теоретическая механика 2 | 200₽ | |||||||||||||||
| 17929 |
Определить глубину потенциальной ямы калия при абсолютном нуле температуры, если работа выхода электронов для него равна A = 2,2 эВ, плотность ρ = 860 кг/м3, молярная масса μ = 0,039 кг/моль. Считать, что число свободных электронов равно числу атомов. |
Физика атома | 200₽ | |||||||||||||||||
| 16549 |
Пространство между двумя большими горизонтальными пластинами заполнено гелием. Расстояние между пластинами 50 мм. На нижней пластине поддерживается температура 290 К, а на верхней – 330 К, гелий находится при нормальном давлении. Для этих условий рассчитать плотность потока тепла в пространстве между плоскостями. |
Молекулярная физика и термодинамика | 200₽ | |||||||||||||||||
| 4369 |
|
Молекулярная физика и термодинамика | 200₽ | |||||||||||||||||
| 13030 |
Задан закон движения $\vec r(t)$ материальной точки в координатной плоскости $XY$ в интервале времени от $t_1$ до $t_2$. Найти уравнение траектории $y=y(x)$ и построить график. Найти модуль вектора перемещения точки в заданном интервале времени. Найти модули начальной $v_1$ и $v_2$ конечной скоростей точки.
|
ФИЗИКА | 1-1-18 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 16747 |
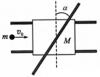
Частица массой m и зарядом q влетает со скоростью v0 в однородное электрическое поле под углом 45° к силовым линиям поля. Оказалось, что через время t частица изменила направление скорости на 90°, сохранив прежней величину скорости. Какова напряжённость E поля? |
Электростатика | 200₽ | |||||||||||||||||
| 13112 |
Частица движется по окружности радиуса R. Угол поворота радиус-вектора частицы меняется со временем по закону φ(t) . Найти число оборотов N, которые частица совершит в интервале времени от t1 до t2. Найти модули векторов тангенциального aτ, нормального an и полного a ускорений, а также угол α между векторами тангенциального и полного ускорений в момент времени t2.
|
ФИЗИКА | 1-3-18 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 13588 |
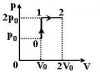
Идеальный газ - азот совершает замкнутый цикл, состоящий из трех процессов 1-2, 2-3 и 3-1, идущий по часовой стрелке. Значения давления и объема газа в состояниях 1, 2 и 3 равны соответственно p1, V1, p2, V2 и p3, V3. Найти термический к.п.д. цикла.
|
ФИЗИКА | 5-2-13 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 4412 |
Смесь, состоящую из 5 кг льда и 15 кг воды при общей температуре 0° С, нужно нагреть до температуры 80° С, пропуская через нее водяной пар, нагретый до 100° С. Определите необходимое количество пара. Удельная теплота плавления льда 3,36∙105 Дж/кг, удельная теплоемкость воды 4190 Дж/(кг∙К), удельная теплота парообразования 2,26∙106 Дж/кг. Ответ представьте в единицах СИ. |
Молекулярная физика и термодинамика | 200₽ | |||||||||||||||||
| 9232 |
Непрерывная случайная величина ξ имеет плотность распределения р(х). |
Теория вероятностей | 200₽ | |||||||||||||||||
| 16674 |
Докажите, что в смеси идеальных газов плотность равна сумме плотностей компонентов смеси: |
Молекулярная физика и термодинамика | 200₽ | |||||||||||||||||
| 13748 |
Пространство между двумя параллельными пластинами площадью S = 300 см2 заполнено газом. Пластины находятся друг от друга на расстоянии h = 5 мм. Одна пластина поддерживается при температуре Т1, другая - при температуре Т2. Найти количество теплоты Q прошедшее посредством теплопроводности от одной пластины к другой за время t = 10 мин. Газ находится при нормальных условиях. Эффективный диаметр молекул газа равен d = 0,36 нм. Показатель адиабаты газа γ.
|
ФИЗИКА | 6-3-13 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 14962 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-66 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | |||||||||||||||
| 13048 |
Частица движется равноускоренно в координатной плоскости $XY$ с начальной скоростью $\vec v_0=A\vec i + B\vec j$ и ускорением $\vec a = C\vec i + D\vec j$. Найти модули векторов скорости v, тангенциального $a_\tau$ и нормального $a_n$ ускорений, а также радиус кривизны траектории $R$ в момент времени $t$.
|
ФИЗИКА | 1-2-6 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 4380 |
|
Молекулярная физика и термодинамика | 200₽ | |||||||||||||||||
| 18199 |
Точка движется в плоскости XOY. Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t в секундах.
|
Теоретическая механика | 200₽ | |||||||||||||||||
| 16641 |
|
Механика | 200₽ | |||||||||||||||||
| 14818 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-01 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | |||||||||||||||
| 13684 |
Идеальный газ находится в однородном поле тяжести Земли. Молярная масса газа М = 29∙10-3 кг/моль. Абсолютная температура газа меняется с высотой h по закону T(h) = T0(l + a∙h). Найти давление газа p на высоте h. На высоте h = 0 давление газа p0 = 105 Па.
|
ФИЗИКА | 6-2-1 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 16682 |
В классе в турнире по армрестлингу каждый сыграл с каждым (ничьих в армрестлинге не бывает). Каждый мальчик одержал вдвое больше побед, чем потерпел поражений, а каждая девочка – вдвое меньше побед, чем поражений. |
МАТЕМАТИКА | 200₽ | |||||||||||||||||
| 11740 |
Используя необходимые и достаточные условия экстремума функционала, исследовать функционал $J(y)$. Если функционал имеет слабый или сильный экстремум, то вычислить экстремальное значение $J^*$. $$J[y]=\int_{0}^{2}(xy'+{y'}^2)dx$$ с граничными условиями $y(0)=1,\ y(2)=0$. |
Вариационное исчисление | 3.1 | Вариационное исчисление | 200₽ | |||||||||||||||
| 14898 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-37,97 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | |||||||||||||||
| 16104 | Электротехника | 200₽ | ||||||||||||||||||
| 14978 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-74 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | |||||||||||||||
| 5167 |
|
Механика | 200₽ | |||||||||||||||||
| 13064 |
Частица движется равноускоренно в координатной плоскости $XY$ с начальной скоростью $\vec v_0=A\vec i + B\vec j$ и ускорением $\vec a = C\vec i + D\vec j$. Найти модули векторов скорости v, тангенциального $a_\tau$ и нормального $a_n$ ускорений, а также радиус кривизны траектории $R$ в момент времени $t$.
|
ФИЗИКА | 1-2-14 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
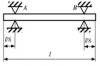
| 14268 | Теоретическая механика | Д5.3 | Теоретическая механика 2 | 200₽ | ||||||||||||||||
| 11588 |
Используя необходимые и достаточные условия экстремума функционала, исследовать функционал $J(y)$. Если функционал имеет слабый или сильный экстремум, то вычислить экстремальное значение $J^*$. $$J[y]=\int_1^2(x^2{y'}^2+12y^2)dx$$ с граничными условиями $y(1)=1,\ y(2)=8$. |
Вариационное исчисление | 3.5 | Вариационное исчисление | 200₽ | |||||||||||||||
| 14834 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-09 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | |||||||||||||||
| 13700 |
Идеальный газ находится в однородном поле тяжести Земли. Молярная масса газа М = 29∙10-3 кг/моль. Абсолютная температура газа меняется с высотой h по закону T(h) = T0(l + a∙h). Найти давление газа p на высоте h. На высоте h = 0 давление газа p0 = 105 Па.
|
ФИЗИКА | 6-2-9 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 16690 | МАТЕМАТИКА | 200₽ | ||||||||||||||||||
| 11756 |
Используя необходимые и достаточные условия экстремума функционала, исследовать функционал $J(y)$. Если функционал имеет слабый или сильный экстремум, то вычислить экстремальное значение $J^*$. $$J[y]=\int_{0}^{1}(y+y')^2 dx$$ с граничными условиями $y(0)=0,\ y(1)=1$. |
Вариационное исчисление | 3.12 | Вариационное исчисление | 200₽ | |||||||||||||||
| 14914 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-45 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | |||||||||||||||
| 5805 |
|
Электромагнетизм | 200₽ | |||||||||||||||||
| 12998 |
Задан закон движения $\vec r(t)$ материальной точки в координатной плоскости $XY$ в интервале времени от $t_1$ до $t_2$. Найти уравнение траектории $y=y(x)$ и построить график. Найти модуль вектора перемещения точки в заданном интервале времени. Найти модули начальной $v_1$ и $v_2$ конечной скоростей точки.
|
ФИЗИКА | 1-1-2 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 14994 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-82 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | |||||||||||||||
| 13080 |
Частица движется по окружности радиуса R. Угол поворота радиус-вектора частицы меняется со временем по закону φ(t) . Найти число оборотов N, которые частица совершит в интервале времени от t1 до t2. Найти модули векторов тангенциального aτ, нормального an и полного a ускорений, а также угол α между векторами тангенциального и полного ускорений в момент времени t2.
|
ФИЗИКА | 1-3-2 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 18216 |
Определить время релаксации τ, среднюю длину свободного пробега λ и дрейфовую vd скорость электрона в электрическом поле E = 2,0 В/см для меди, если его теплопроводность k равна 390 Вт/(м·К). |
Квантовая физика | 200₽ | |||||||||||||||||
| 14850 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-17 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | |||||||||||||||
| 13716 |
Идеальный газ находится в однородном поле тяжести Земли. Молярная масса газа М = 29∙10-3 кг/моль. Абсолютная температура газа меняется с высотой h по закону T(h) = T0(l + a∙h). Найти давление газа p на высоте h. На высоте h = 0 давление газа p0 = 105 Па.
|
ФИЗИКА | 6-2-17 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 11772 |
Используя необходимые и достаточные условия экстремума функционала, исследовать функционал $J(y)$. Если функционал имеет слабый или сильный экстремум, то вычислить экстремальное значение $J^*$. $$J[y]=\int_1^2y'(y+x^2y')dx$$ с граничными условиями $y(1)=0,\ y(2)=1/2$. |
Вариационное исчисление | 3.21 | Вариационное исчисление | 200₽ | |||||||||||||||
| 14930 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-53 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | |||||||||||||||
| 13014 |
Задан закон движения $\vec r(t)$ материальной точки в координатной плоскости $XY$ в интервале времени от $t_1$ до $t_2$. Найти уравнение траектории $y=y(x)$ и построить график. Найти модуль вектора перемещения точки в заданном интервале времени. Найти модули начальной $v_1$ и $v_2$ конечной скоростей точки.
|
ФИЗИКА | 1-1-10 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 13096 |
Частица движется по окружности радиуса R. Угол поворота радиус-вектора частицы меняется со временем по закону φ(t) . Найти число оборотов N, которые частица совершит в интервале времени от t1 до t2. Найти модули векторов тангенциального aτ, нормального an и полного a ускорений, а также угол α между векторами тангенциального и полного ускорений в момент времени t2.
|
ФИЗИКА | 1-3-10 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 13572 |
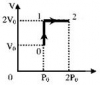
Идеальный газ - азот совершает замкнутый цикл, состоящий из трех процессов 1-2, 2-3 и 3-1, идущий по часовой стрелке. Значения давления и объема газа в состояниях 1, 2 и 3 равны соответственно p1, V1, p2, V2 и p3, V3. Найти термический к.п.д. цикла.
|
ФИЗИКА | 5-2-5 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | |||||||||||||||
| 4404 |
Тепловой двигатель за счет каждого килоджоуля теплоты, полученной от теплоотдатчика в течение каждого цикла, совершает работу, равную 430 Дж. Определить термический КПД машины и температуру теплоотдатчика. если температура теплоприемника равна 280 К. |
Молекулярная физика и термодинамика | 200₽ |