Если найти нужную задачу не удаётся, Вы можете оформить Заказ.
Как использовать поиск
| Номер | Условие задачи | Предмет | Задачник |
Цена |
|||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 14980 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-75 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | ||||||||||||||||||||
| 13066 |
Частица движется равноускоренно в координатной плоскости $XY$ с начальной скоростью $\vec v_0=A\vec i + B\vec j$ и ускорением $\vec a = C\vec i + D\vec j$. Найти модули векторов скорости v, тангенциального $a_\tau$ и нормального $a_n$ ускорений, а также радиус кривизны траектории $R$ в момент времени $t$.
|
ФИЗИКА | 1-2-15 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | ||||||||||||||||||||
| 14270 | Теоретическая механика | 200₽ | |||||||||||||||||||||||
| 11590 |
Используя необходимые и достаточные условия экстремума функционала, исследовать функционал $J(y)$. Если функционал имеет слабый или сильный экстремум, то вычислить экстремальное значение $J^*$. $$J[y]=\int_0^1(xy^2+x^2yy'+(1+x^2){y'}^2)dx$$ с граничными условиями $y(0)=0,\ y(1)=1$. |
Вариационное исчисление | 3.11 | Вариационное исчисление | 200₽ | ||||||||||||||||||||
| 6735 |
Необходимо определить зависимости математического ожидания (среднего значения) износа деталей y(t) и дисперсии D(y(t)) от пробега (наработки), используя данные из таблицы 5. Параметры искомых зависимостей следует рассчитать с использованием правила определения прямой, проходящей через две точки с известными координатами.
Задание 6 контрольной работы "Надежность подвижного состава" |
Теория вероятностей | 200₽ | ||||||||||||||||||||||
| 4405 |
Сколько молекул кислорода содержится в объеме 10 м3, если при хаотическом движении со средней скоростью квадратичной 400 м/с они производят на стенки сосуда давление в 104 Па? |
Молекулярная физика и термодинамика | 200₽ | ||||||||||||||||||||||
| 16650 |
Снаряд, выпущенный вертикально вверх, мгновенно разрывается в высшей точке траектории на два осколка, массы которых m1 = 10 кг и m2 = 20 кг. Скорость лёгкого осколка сразу после взрыва v1 = 1000 м/с. |
Механика | 200₽ | ||||||||||||||||||||||
| 14836 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-10 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | ||||||||||||||||||||
| 18251 |
На газовой плите стоит цилиндрическая кастрюля с площадью поперечного сечения S = 200 см2, в которой кипятятся 2 литра воды. Если подвод теплоты от горелки не меняется с течением времени, то за 10 минут выкипает слой воды толщиной h = 1 см. В кастрюлю начинают бросать с постоянной скоростью маленькие шарики льда, имеющие температуру t = 0 °C. Какую массу M таких шариков в минуту надо бросать для поддержания постоянного уровня кипящей воды в этой кастрюле? |
Молекулярная физика и термодинамика | 200₽ | ||||||||||||||||||||||
| 13702 |
Идеальный газ находится в однородном поле тяжести Земли. Молярная масса газа М = 29∙10-3 кг/моль. Абсолютная температура газа меняется с высотой h по закону T(h) = T0(l + a∙h). Найти давление газа p на высоте h. На высоте h = 0 давление газа p0 = 105 Па.
|
ФИЗИКА | 6-2-10 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | ||||||||||||||||||||
| 16691 |
Петя, Вася и Толя на уроке физкультуры по очереди бросают друг другу волейбольный мяч. Первым его бросает Петя. Найдите число способов, которыми мяч может вернуться обратно к Пете через 23 броска (не обязательно впервые). |
МАТЕМАТИКА | 200₽ | ||||||||||||||||||||||
| 11758 |
Используя необходимые и достаточные условия экстремума функционала, исследовать функционал $J(y)$. Если функционал имеет слабый или сильный экстремум, то вычислить экстремальное значение $J^*$. $$J[y]=\int_{0}^{1}({y'}^2-y^2+8xy)dx$$ с граничными условиями $y(0)=0,\ y(1)=5$. |
Вариационное исчисление | 3.14 | Вариационное исчисление | 200₽ | ||||||||||||||||||||
| 14916 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-46 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | ||||||||||||||||||||
| 13000 |
Задан закон движения $\vec r(t)$ материальной точки в координатной плоскости $XY$ в интервале времени от $t_1$ до $t_2$. Найти уравнение траектории $y=y(x)$ и построить график. Найти модуль вектора перемещения точки в заданном интервале времени. Найти модули начальной $v_1$ и $v_2$ конечной скоростей точки.
|
ФИЗИКА | 1-1-3 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | ||||||||||||||||||||
| 14996 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-83 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | ||||||||||||||||||||
| 13082 |
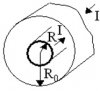
Частица движется по окружности радиуса R. Угол поворота радиус-вектора частицы меняется со временем по закону φ(t) . Найти число оборотов N, которые частица совершит в интервале времени от t1 до t2. Найти модули векторов тангенциального aτ, нормального an и полного a ускорений, а также угол α между векторами тангенциального и полного ускорений в момент времени t2.
|
ФИЗИКА | 1-3-3 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | ||||||||||||||||||||
| 10326 |
|
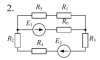
Электротехника | 292 | МИИТ. Общая электротехника и электроника. 2016 год | 200₽ | ||||||||||||||||||||
| 16374 |
|
Электростатика | 4-3-9 | ТГУ. Физика | 200₽ | ||||||||||||||||||||
| 6751 |
Необходимо определить зависимости математического ожидания (среднего значения) износа деталей y(t) и дисперсии D(y(t)) от пробега (наработки), используя данные из таблицы 5. Параметры искомых зависимостей следует рассчитать с использованием правила определения прямой, проходящей через две точки с известными координатами.
Задание 6 контрольной работы "Надежность подвижного состава" |
Теория вероятностей | 200₽ | ||||||||||||||||||||||
| 18217 |
Удельная электропроводность меди при комнатной температуре 5,9∙107 Ом-1∙м-1, плотность 8,9∙103 кг/м3, энергия Ферми 6,2 эВ. Определить среднюю скорость, время релаксации, длину свободного пробега и концентрацию электронов проводимости в меди при абсолютном нуле, а также дрейфовую скорость электронов при напряжённости внешнего поля 100 В/см. |
Квантовая физика | 200₽ | ||||||||||||||||||||||
| 14852 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-18 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | ||||||||||||||||||||
| 13718 |
Идеальный газ находится в однородном поле тяжести Земли. Молярная масса газа М = 29∙10-3 кг/моль. Абсолютная температура газа меняется с высотой h по закону T(h) = T0(l + a∙h). Найти давление газа p на высоте h. На высоте h = 0 давление газа p0 = 105 Па.
|
ФИЗИКА | 6-2-18 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | ||||||||||||||||||||
| 16700 |
Точки P, Q, R лежат соответственно на сторонах AB, BC, AC треугольника ABC, причём AP:PB = 2:5, BQ:QC = 1:4, а площадь треугольника PQR составляет 31/70 площади треугольника ABC. Найдите AR:RC. |
Геометрия | 200₽ | ||||||||||||||||||||||
| 11774 |
Используя необходимые и достаточные условия экстремума функционала, исследовать функционал $J(y)$. Если функционал имеет слабый или сильный экстремум, то вычислить экстремальное значение $J^*$. |
Вариационное исчисление | 3.22 | Вариационное исчисление | 200₽ | ||||||||||||||||||||
| 14932 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-54 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | ||||||||||||||||||||
| 8978 |
Газ массой G содержится в цилиндре под поршнем площадью F. Начальная высота газового объема Y1. Вследствие нагревания газа поршень поднимается в цилиндре до высоты Y2. При этом поршень давит на газ с постоянной силой Pсил. Определить работу и теплопоток в процессе расширения газа, а также термические параметры газа - давление, удельный объем, температуру (p, V, T) до и после процесса и изменение калорических параметров в процессе - удельной внутренней энергии, удельной энтальпии, удельной энтропии (ΔU, Δi, ΔS). Представить графически процесс расширения газа в pV-диаграмме.
|
Теплотехника | 200₽ | ||||||||||||||||||||||
| 13016 |
Задан закон движения $\vec r(t)$ материальной точки в координатной плоскости $XY$ в интервале времени от $t_1$ до $t_2$. Найти уравнение траектории $y=y(x)$ и построить график. Найти модуль вектора перемещения точки в заданном интервале времени. Найти модули начальной $v_1$ и $v_2$ конечной скоростей точки.
|
ФИЗИКА | 1-1-11 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | ||||||||||||||||||||
| 16740 |
Для нагревания 200 г некоторого газа на 4 °C в процессе, в котором давление прямо пропорционально объему, требуется на 831 Дж большее тепла, чем для такого же нагревания при постоянном объеме. Что это за газ? |
Молекулярная физика и термодинамика | 200₽ | ||||||||||||||||||||||
| 13098 |
Частица движется по окружности радиуса R. Угол поворота радиус-вектора частицы меняется со временем по закону φ(t) . Найти число оборотов N, которые частица совершит в интервале времени от t1 до t2. Найти модули векторов тангенциального aτ, нормального an и полного a ускорений, а также угол α между векторами тангенциального и полного ускорений в момент времени t2.
|
ФИЗИКА | 1-3-11 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | ||||||||||||||||||||
| 13574 |
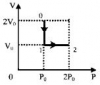
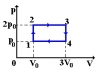
Идеальный газ - азот совершает замкнутый цикл, состоящий из трех процессов 1-2, 2-3 и 3-1, идущий по часовой стрелке. Значения давления и объема газа в состояниях 1, 2 и 3 равны соответственно p1, V1, p2, V2 и p3, V3. Найти термический к.п.д. цикла.
|
ФИЗИКА | 5-2-6 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | ||||||||||||||||||||
| 4381 |
|
Молекулярная физика и термодинамика | 200₽ | ||||||||||||||||||||||
| 14868 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-26 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | ||||||||||||||||||||
| 13734 |
Пространство между двумя параллельными пластинами площадью S = 300 см2 заполнено газом. Пластины находятся друг от друга на расстоянии h = 5 мм. Одна пластина поддерживается при температуре Т1, другая - при температуре Т2. Найти количество теплоты Q прошедшее посредством теплопроводности от одной пластины к другой за время t = 10 мин. Газ находится при нормальных условиях. Эффективный диаметр молекул газа равен d = 0,36 нм. Показатель адиабаты газа γ.
|
ФИЗИКА | 6-3-6 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | ||||||||||||||||||||
| 13032 |
Задан закон движения $\vec r(t)$ материальной точки в координатной плоскости $XY$ в интервале времени от $t_1$ до $t_2$. Найти уравнение траектории $y=y(x)$ и построить график. Найти модуль вектора перемещения точки в заданном интервале времени. Найти модули начальной $v_1$ и $v_2$ конечной скоростей точки.
|
ФИЗИКА | 1-1-19 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | ||||||||||||||||||||
| 16748 |
В плоский конденсатор расстояние, между пластинами которого равно d, внесли n = 50 пластин диэлектрической проницаемостью ε = 5 и толщиной 0,01d каждая и расположили их параллельно обкладкам на равном расстоянии друг от друга. Во сколько раз изменится ёмкость конденсатора? |
Электростатика | 200₽ | ||||||||||||||||||||||
| 13114 |
Частица движется по окружности радиуса R. Угол поворота радиус-вектора частицы меняется со временем по закону φ(t) . Найти число оборотов N, которые частица совершит в интервале времени от t1 до t2. Найти модули векторов тангенциального aτ, нормального an и полного a ускорений, а также угол α между векторами тангенциального и полного ускорений в момент времени t2.
|
ФИЗИКА | 1-3-19 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | ||||||||||||||||||||
| 13590 |
Идеальный газ - азот совершает замкнутый цикл, состоящий из трех процессов 1-2, 2-3 и 3-1, идущий по часовой стрелке. Значения давления и объема газа в состояниях 1, 2 и 3 равны соответственно p1, V1, p2, V2 и p3, V3. Найти термический к.п.д. цикла.
|
ФИЗИКА | 5-2-14 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | ||||||||||||||||||||
| 14884 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-30 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | ||||||||||||||||||||
| 13750 |
Пространство между двумя параллельными пластинами площадью S = 300 см2 заполнено газом. Пластины находятся друг от друга на расстоянии h = 5 мм. Одна пластина поддерживается при температуре Т1, другая - при температуре Т2. Найти количество теплоты Q прошедшее посредством теплопроводности от одной пластины к другой за время t = 10 мин. Газ находится при нормальных условиях. Эффективный диаметр молекул газа равен d = 0,36 нм. Показатель адиабаты газа γ.
|
ФИЗИКА | 6-3-14 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | ||||||||||||||||||||
| 14964 |
Точка B движется в плоскости (x,y). Закон движения точки задан уравнениями: x = f1(t); y = f2(t), где x и y выражены в сантиметрах, t - в секундах.
(х, у - в сантиметрах, t - в секундах). |
Теоретическая механика | К1-67 | Методичка по термеху. Нижний Новгород. 2019 год | 200₽ | ||||||||||||||||||||
| 13050 |
Частица движется равноускоренно в координатной плоскости $XY$ с начальной скоростью $\vec v_0=A\vec i + B\vec j$ и ускорением $\vec a = C\vec i + D\vec j$. Найти модули векторов скорости v, тангенциального $a_\tau$ и нормального $a_n$ ускорений, а также радиус кривизны траектории $R$ в момент времени $t$.
|
ФИЗИКА | 1-2-7 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | ||||||||||||||||||||
| 13450 |
Один моль идеального газа переходит из начального состояния 1 в конечное состояние 3 в результате двух изопроцессов 1-2 и 2-3. Значения давления и объема газа в состояниях 1 и 3 равны соответственно p1, V1 и p3, V3. Найти давление, объем и температуру газа p2, V2, T2 в промежуточном состоянии 2. Изобразить процессы в координатах p-V, p-T и V-T.
|
ФИЗИКА | 4-2-4 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | ||||||||||||||||||||
| 14742 |
|
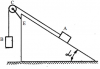
Теоретическая механика | Д4.2 | Теоретическая механика 2 | 200₽ | ||||||||||||||||||||
| 8758 |
|
Электромагнетизм | 200₽ | ||||||||||||||||||||||
| 13466 |
Один моль идеального газа переходит из начального состояния 1 в конечное состояние 3 в результате двух изопроцессов 1-2 и 2-3. Значения давления и объема газа в состояниях 1 и 3 равны соответственно p1, V1 и p3, V3. Найти давление, объем и температуру газа p2, V2, T2 в промежуточном состоянии 2. Изобразить процессы в координатах p-V, p-T и V-T.
|
ФИЗИКА | 4-2-12 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | ||||||||||||||||||||
| 12756 |
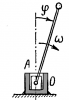
Материальная точка движется по окружности радиуса R так, что зависимость угла поворота φ от времени $\varphi =a+bt+ct^2$. Определить для момента времени t1 c линейную и угловую скорости точки; нормальное, тангенциальное и полное ускорения точки, а для промежутка времени t1 c до t2 c перемещение точки и пройденный путь.
|
Механика | 2-8 | ЗабГУ. Физика. 2011 год | 200₽ | ||||||||||||||||||||
| 4367 | Молекулярная физика и термодинамика | 200₽ | |||||||||||||||||||||||
| 16807 |
|
Комбинаторика | 200₽ | ||||||||||||||||||||||
| 16534 |
Воздушный шар начинает подниматься с поверхности земли. Скорость его подъема постоянна и равна v0. Благодаря ветру, шар приобретает горизонтальную компоненту скорости vx = αy, где α - постоянная величина, у - высота подъема. |
Механика | 200₽ | ||||||||||||||||||||||
| 13482 |
Один моль идеального газа переходит из начального состояния 1 в конечное состояние 3 в результате двух изопроцессов 1-2 и 2-3. Значения давления и объема газа в состояниях 1 и 3 равны соответственно p1, V1 и p3, V3. Найти давление, объем и температуру газа p2, V2, T2 в промежуточном состоянии 2. Изобразить процессы в координатах p-V, p-T и V-T.
|
ФИЗИКА | 4-2-20 | ТГУ. Практические занятия по физике. 2019 год | 200₽ | ||||||||||||||||||||