Онлайн-магазин готовых решений

Вы можете мгновенно получить на свой е-мэйл решение любой из этих задач, оплатив её стоимость через онлайн-сервис на нашем сайте. Подробные инструкции по оплате можно увидеть, кликнув на ссылку номера задачи.
Если найти нужную задачу не удаётся, Вы можете оформить Заказ.

Как использовать поиск
Всего задач, соответствующих запросу: 8041
Номер Условие задачи Предмет Задачник Ценасортировать по убыванию
9732

Даны вершины $A_1(1,8,2), А_2(4,-1,2), А_3(-1,5,3), А_4(3,3,-3)$ пирамиды:
Построить пирамиду в декартовой ортонормированной системе координат.
Найти:
1) длину ребра $А_1А_2$;
2) угол между ребрами $А_1А_2$ и $А_1А_4$;
3) уравнение грани $A_1A_2A_3$ и ее площадь;
4) уравнения высоты, опущенной из вершины $A_4$ на грань $А_1А_2А_3$.

 Аналитическая геометрия 150₽
11814

Найти экстремали функционалов от вектор - функции.
$$J[y_1,y_2]=\int_0^1(y_1^2+y_2^2+2y'_1y'_2)dx,$$ $$y_1(0)=1;\ y_1(1)=\frac{e+e^{-1}}{2},\ y_2(0)=1,\ y_2(1)=\frac{e+e^{-1}}{2}$$

 Вариационное исчисление 4.11 Вариационное исчисление 150₽
14176




Круглая платформа (рис.6) радиусом R = 0,4 м вращается вокруг неподвижной оси О по закону φ = 3t2 - 4t (рад). По окружности пластины движется точка M. Закон его относительного движения S = 4πt2 (см). Определить абсолютную скорость и ускорение точки в момент времени t1 = 1 c.

 Теоретическая механика D3.21 МИИТ. Теоретическая механика. 2012 год 150₽
13532

Один моль идеального газа переходит из начального состояния 1 в конечное состояние 3 в результате двух процессов 1-2 и 2-3. Значения давления и объема газа в состояниях 1 и 3 равны соответственно P1, V1 и P3, V3. Найти работу, совершенную газом, количество теплоты Q, полученное газом и приращение внутренней энергии газа ΔU в процессе перехода из начального состояния 1 в конечное состояние 3.

№ варианта газ, процессы, P1, V1, P3, V3
5 изобарный 1-2, газ - N2, P1 = 105 Па, V1 = 3 л, изотермический 2-3, P3 = 2∙105 Па, V3 = 6 л
ФИЗИКА 5-1-5 ТГУ. Практические занятия по физике. 2019 год 150₽
17870

Вычислить интеграл $$\oint\limits_{x^2+y^2=1} \frac{(z+1) dz}{z^2+2z-3}$$

 Теория функций комплексного переменного 150₽
9176

Найти экстремали функционалов: с дифференциальными связями:
$$J[y_1,y_2]=\int_0^{\pi}(y_1'^2-y_2^2)dx;$$
$$y_1(0)=-1, y_1(\pi)=1, y_2(0)=0, y_2(\pi)=-\pi, y_1'-y_2-2\sin x=0$$

 Вариационное исчисление 4.13 Вариационное исчисление 150₽
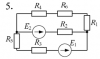
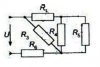
10462




Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии.
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 2, выполнить следующее:
1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений не следует.
2. Определить токи в ветвях методом контурных токов.
3. Определить режимы работы активных элементов и составить баланс мощностей.
Значения ЭДС источников и сопротивлений приемников приведены в табл. 2.

Предпоследняя цифра учебного шифра студента E1, В E2, В R1, Ом R2, Ом R3, Ом R4, Ом R5, Ом R6, Ом
4 90 170 6 11 15 20 12 13
Электротехника 245 МИИТ. Общая электротехника и электроника. 2016 год 150₽
14432

Космический объект с массой покоя m0 движется со скоростью V имея импульс Р и кинетическую энергию Т. Собственная длина объекта в направлении движения l0, релятивистское изменение этой длины Δl. Определить параметры, обозначенные для Вашего варианта знаком “?"

№ варианта m0, кг V, Мм/с P, 1011 кг∙м/с T, 1022 Дж l0, м Δl, м
2 3000 ? ? 1,08 3 ?
Специальная теория относительности 7-2 ЗабГУ. Физика. 2011 год 150₽
10542




Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии.
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 2, выполнить следующее:
1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений не следует.
2. Определить токи в ветвях методом контурных токов.
3. Определить режимы работы активных элементов и составить баланс мощностей.
Значения ЭДС источников и сопротивлений приемников приведены в табл. 2.

Предпоследняя цифра учебного шифра студента E1, В E2, В R1, Ом R2, Ом R3, Ом R4, Ом R5, Ом R6, Ом
3 80 180 11 7 12 16 21 13
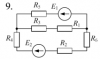
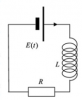
Электротехника 239 МИИТ. Общая электротехника и электроника. 2016 год 150₽
12908

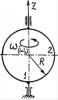
Диск массой m, имеющий радиус R, начинает вращаться под действием силы F, приложенной по касательной к образующей диска, перпендикулярно ею радиусу; при этом момент сил трения, действующий на диск, равен М1. За время t, отсчитанное oт начала движения, диск совершает N оборотов. Определить параметр, обозначенный в таблице данных для Вашего варианта знаком «?».

Номер варианта m, кг R, м F, Н M1, Н∙м t, сек N
7 ? 0,5 12 4 15 7
Механика 5-7 ЗабГУ. Физика. 2011 год 150₽
12090




САМОСТОЯТЕЛЬНАЯ РАБОТА 1
Вариант 69.
Расчёт разветвлённой электрической цепи постоянного тока
Для данной электрической цепи определить с использованием законов Ома и Кирхгофа
1. Токи в ветвях
2. Мощность, развиваемую источником энергии, и мощность потребителей
3. Составить баланс мощности

Последняя цифра номера студенческого билета U, В R1, Ом R2, Ом R2, Ом R4, Ом R5, Ом
9 127 8 7 4 17 12
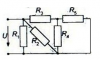
Электротехника 69 Разветвлённая электрическая цепь постоянного тока 150₽
17914

Вычислить несобственный интеграл, используя вычеты: $$\int\limits_{-\infty}^{+\infty} \frac{x\sin{2x}}{(x^2-2x+5)^2}dx$$

 Теория функций комплексного переменного 150₽
14518

Космический объект с массой покоя m0 движется со скоростью V имея импульс Р и кинетическую энергию Т. Собственная длина объекта в направлении движения l0, релятивистское изменение этой длины Δl. Определить параметры, обозначенные для Вашего варианта знаком “?"

№ варианта m0, кг V, Мм/с P, 1011 кг∙м/с T, 1022 Дж l0, м Δl, м
6 3000 ? 5,196 ? ? 0,402
Специальная теория относительности 7-6 ЗабГУ. Физика. 2011 год 150₽
14682

Автомобиль массой m из состояния покоя начинает преодолевать подъём с углом наклона α к горизонту. Найти закон изменения скорости автомобиля от величины пройденного пути, если сила тяги двигателя F является постоянной величиной. Другими видами сопротивления пренебречь.

Теоретическая механика Д2.9 Теоретическая механика 2 150₽
18173

Автомобиль преодолевает подъём с углом наклона α. Коэффициент трения колёс о дорогу равен f. Определить тормозной путь автомобиля, если его скорость в момент отключения двигателя и включения тормозного привода была равна v0. Колёса автомобиля считать полностью заторможенными.

 Кинематика 150₽
12016




САМОСТОЯТЕЛЬНАЯ РАБОТА 1
Вариант 37.
Расчёт разветвлённой электрической цепи постоянного тока
Для данной электрической цепи определить с использованием законов Ома и Кирхгофа
1. Токи в ветвях
2. Мощность, развиваемую источником энергии, и мощность потребителей
3. Составить баланс мощности

Последняя цифра номера студенческого билета U, В R1, Ом R2, Ом R2, Ом R4, Ом R5, Ом
7 110 15 20 18 12 14
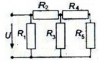
Электротехника 37 Разветвлённая электрическая цепь постоянного тока 150₽
8880

Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям: $$\newcommand{\ctg}{\mathop{\mathrm{ctg}}\nolimits}J[y]=\int_{\pi/3}^{\pi/2}({y'}^2-y^2-2y\ctg{x})dx;\ y(\pi/3)=\frac{\sqrt{3}\ln{3}}{4},\ y(\pi/2)=0$$

 Вариационное исчисление 2.9 Вариационное исчисление 150₽
12106




САМОСТОЯТЕЛЬНАЯ РАБОТА 1
Вариант 77.
Расчёт разветвлённой электрической цепи постоянного тока
Для данной электрической цепи определить с использованием законов Ома и Кирхгофа
1. Токи в ветвях
2. Мощность, развиваемую источником энергии, и мощность потребителей
3. Составить баланс мощности

Последняя цифра номера студенческого билета U, В R1, Ом R2, Ом R2, Ом R4, Ом R5, Ом
7 110 15 20 18 12 14
Электротехника 77 Разветвлённая электрическая цепь постоянного тока 150₽
14534

Космический объект с массой покоя m0 движется со скоростью V имея импульс Р и кинетическую энергию Т. Собственная длина объекта в направлении движения l0, релятивистское изменение этой длины Δl. Определить параметры, обозначенные для Вашего варианта знаком “?"

№ варианта m0, кг V, Мм/с P, 1011 кг∙м/с T, 1022 Дж l0, м Δl, м
14 1200 ? 4.03 ? ? 1.144
Специальная теория относительности 7-14 ЗабГУ. Физика. 2011 год 150₽
18056

Разложить функцию $f(x)$ в ряд Фурье в указанном интервале. Выписать полученный ряд и три первых члена разложения отдельно. Построить графики функции $f(x)$ и её приближения: $$f(x)=x-3 \ в \ интервале \ (-\pi;\pi)$$

 Ряды 150₽
13408

В сосуде объемом V при температуре T находится смесь двух идеальных газов с массами m1 и m2. Найти давление смеси p, молярную массу смеси M и число молекул в N сосуде.

№ варианта газы, V, T, m1, m2
3 N2 - m1 = 150 г, He - m2 = 100 г, V = 3 л, T = 300 К
ФИЗИКА 4-1-3 ТГУ. Практические занятия по физике. 2019 год 150₽
12596




САМОСТОЯТЕЛЬНАЯ РАБОТА 1
Вариант 23.
Расчёт разветвлённой электрической цепи постоянного тока
Для данной электрической цепи определить с использованием законов Ома и Кирхгофа
1. Токи в ветвях
2. Мощность, развиваемую источником энергии, и мощность потребителей
3. Составить баланс мощности

Последняя цифра номера студенческого билета U, В R1, Ом R2, Ом R2, Ом R4, Ом R5, Ом
3 42 6 9 7 11 12
Электротехника 23 Разветвлённая электрическая цепь постоянного тока 150₽
13488

Один моль идеального газа совершает процесс, в котором давление газа P убывает с увеличением его объема V по заданному закону P(V). Найти максимальную температуру газа в этом процессе.

№ варианта P(V)
3 P(V) = P0 - aV2, P0 = 2∙104 Па, a = 4∙106 Па∙м-6
ФИЗИКА 4-3-3 ТГУ. Практические занятия по физике. 2019 год 150₽
14698




Круглый цилиндр A массой m обмотан посредине тонкой нитью, конец которой закреплен неподвижно. Цилиндр падает вертикально вниз, разматывая нить. Ускорение оси C цилиндра равно ac = 0,4g. Найти натяжение нити.

 Теоретическая механика Д4.10 Теоретическая механика 2 150₽
11944




САМОСТОЯТЕЛЬНАЯ РАБОТА 1
Вариант 04.
Расчёт разветвлённой электрической цепи постоянного тока
Для данной электрической цепи определить с использованием законов Ома и Кирхгофа
1. Токи в ветвях
2. Мощность, развиваемую источником энергии, и мощность потребителей
3. Составить баланс мощности

Последняя цифра номера студенческого билета U, В R1, Ом R2, Ом R2, Ом R4, Ом R5, Ом
4 36 8 3 4 5 6
Электротехника 04 Разветвлённая электрическая цепь постоянного тока 150₽
8800

Найти все экстремали функционала J(y),
$$J[y]=\int_{1}^{\pi}(y'^2-y^2)dx,$$ удовлетворяющие граничным условиям $y(0)=1; y(\pi)=-1$

 Вариационное исчисление 2.18 Вариационное исчисление 150₽
12040




САМОСТОЯТЕЛЬНАЯ РАБОТА 1
Вариант 45.
Расчёт разветвлённой электрической цепи постоянного тока
Для данной электрической цепи определить с использованием законов Ома и Кирхгофа
1. Токи в ветвях
2. Мощность, развиваемую источником энергии, и мощность потребителей
3. Составить баланс мощности

Последняя цифра номера студенческого билета U, В R1, Ом R2, Ом R2, Ом R4, Ом R5, Ом
5 90 10 14 12 9 13
Электротехника 45 Разветвлённая электрическая цепь постоянного тока 150₽
17889

Вычислить интеграл $$\oint\limits_{|z+i|=1} \frac{e^z}{z^4+2z^2+1 }dz$$

 Теория функций комплексного переменного 150₽
8906

Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям. $$J[y]=\int_{-1}^{0}({y'}^2-2xy)dx;\ y(-1)=0;\ y(0)=2$$

 Вариационное исчисление 2.5 Вариационное исчисление 150₽
12126




САМОСТОЯТЕЛЬНАЯ РАБОТА 1
Вариант 85.
Расчёт разветвлённой электрической цепи постоянного тока
Для данной электрической цепи определить с использованием законов Ома и Кирхгофа
1. Токи в ветвях
2. Мощность, развиваемую источником энергии, и мощность потребителей
3. Составить баланс мощности

Последняя цифра номера студенческого билета U, В R1, Ом R2, Ом R2, Ом R4, Ом R5, Ом
5 90 10 14 12 9 13
Электротехника 85 Разветвлённая электрическая цепь постоянного тока 150₽
16068

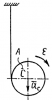
Два одинаковых круговых проволочных витка радиусом R касаются друг друга так, что угол между плоскостями витков равен α. По виткам текут в одном направлении, по часовой стрелке, токи I1 и I2. Напряжённость магнитного поля, созданного этими токами в точке пересечения осей витков, равна Н. Определить параметр, обозначенный в таблице для Вашего варианта знаком «?».

Вариант R, см α, ° I1, A I2, A H, А/м
5 10 75 40 50 ?
Электродинамика 2-4-5 ЗабГУ. Физика. 2011 год 150₽
17930

Определить глубину потенциальной ямы лития при абсолютном нуле температуры, если работа выхода электронов для него равна A = 2,3 эВ, плотность ρ = 534 кг/м3, молярная масса μ = 0,0069 кг/моль. Считать, что число свободных электронов равно числу атомов.

 Физика атома 150₽
14550

Космический объект с массой покоя m0 движется со скоростью V имея импульс Р и кинетическую энергию Т. Собственная длина объекта в направлении движения l0, релятивистское изменение этой длины Δl. Определить параметры, обозначенные для Вашего варианта знаком “?"

№ варианта m0, кг V, Мм/с P, 1011 кг∙м/с T, 1022 Дж l0, м Δl, м
22 3000 150 ? ? ? 0.8
Специальная теория относительности 7-22 ЗабГУ. Физика. 2011 год 150₽
13424

В сосуде объемом V при температуре T находится смесь двух идеальных газов с массами m1 и m2. Найти давление смеси p, молярную массу смеси M и число молекул в N сосуде.

№ варианта газы, V, T, m1, m2
11 N2 - m1 = 150 г, H2 - m2 = 100 г, V = 3 л, T = 300 К
ФИЗИКА 4-1-11 ТГУ. Практические занятия по физике. 2019 год 150₽
13504

Один моль идеального газа совершает процесс, в котором давление газа P убывает с увеличением его объема V по заданному закону P(V). Найти максимальную температуру газа в этом процессе.

№ варианта P(V)
11 P(V) = P0e-bV, P0 = 105 Па, b = 15 м-3
ФИЗИКА 4-3-11 ТГУ. Практические занятия по физике. 2019 год 150₽
11960




САМОСТОЯТЕЛЬНАЯ РАБОТА 1
Вариант 12.
Расчёт разветвлённой электрической цепи постоянного тока
Для данной электрической цепи определить с использованием законов Ома и Кирхгофа
1. Токи в ветвях
2. Мощность, развиваемую источником энергии, и мощность потребителей
3. Составить баланс мощности

Последняя цифра номера студенческого билета U, В R1, Ом R2, Ом R2, Ом R4, Ом R5, Ом
2 220 16 23 19 18 20
Электротехника 12 Разветвлённая электрическая цепь постоянного тока 150₽
15922




Электрическая цепь состоит из катушки индуктивностью L резистора сопротивлением R и источника тока, ЭДС которого меняется со временем по заданному закону
$$E(t)= E_0(1-e^\frac{-t}{\tau})$$
Найти зависимость от времени силы тока I(t) в цепи.

 Электродинамика 150₽
8816

Найти все экстремали функционала J(y),
$$J[y]=\int_0^e(x^3y'^2-xy^2)dx,$$ удовлетворяющие граничным условиям $y(1)=0; y(e)=1/e$

 Вариационное исчисление 1.8 Вариационное исчисление 150₽
12058




САМОСТОЯТЕЛЬНАЯ РАБОТА 1
Вариант 53.
Расчёт разветвлённой электрической цепи постоянного тока
Для данной электрической цепи определить с использованием законов Ома и Кирхгофа
1. Токи в ветвях
2. Мощность, развиваемую источником энергии, и мощность потребителей
3. Составить баланс мощности

Последняя цифра номера студенческого билета U, В R1, Ом R2, Ом R2, Ом R4, Ом R5, Ом
3 42 6 9 7 11 12
Электротехника 53 Разветвлённая электрическая цепь постоянного тока 150₽
17898

Вычислить несобственный интеграл, используя вычеты: $$\int\limits_{-\infty}^{+\infty} \frac{x\sin {x}}{(x^2+4)(x^2+1)}dx$$

 Теория функций комплексного переменного 150₽
12144




САМОСТОЯТЕЛЬНАЯ РАБОТА 1
Вариант 93.
Расчёт разветвлённой электрической цепи постоянного тока
Для данной электрической цепи определить с использованием законов Ома и Кирхгофа
1. Токи в ветвях
2. Мощность, развиваемую источником энергии, и мощность потребителей
3. Составить баланс мощности

Последняя цифра номера студенческого билета U, В R1, Ом R2, Ом R2, Ом R4, Ом R5, Ом
3 42 6 9 7 11 12
Электротехника 93 Разветвлённая электрическая цепь постоянного тока 150₽
16486

Бусинка массы m надета на гладкое проволочное кольцо радиуса R = 2 м, плоскость которого наклонена под углом α = 30° к горизонту. Кольцо жесткое и закреплено неподвижно. В некоторый момент бусинка начинает движение из верхней точки кольца с пренебрежимо малой скоростью. Найдите ускорение a бусинки в нижней точке кольца (укажите величину и направление). С какой по величине силой N действует кольцо на бусинку в момент прохождения нижней точки кольца. Какой угол β образует сила N с вертикалью?

 Механика 150₽
13440

В сосуде объемом V при температуре T находится смесь двух идеальных газов с массами m1 и m2. Найти давление смеси p, молярную массу смеси M и число молекул в N сосуде.

№ варианта газы, V, T, m1, m2
19 H2 - m1 = 150 г, CH4 - m2 = 100 г, V = 3 л, T = 300 К
ФИЗИКА 4-1-19 ТГУ. Практические занятия по физике. 2019 год 150₽
14732




ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОГО МОМЕНТА.
Кольцевая трубка массой M и радиусом R вращается вокруг вертикальной оси с угловой скоростью ω0. Внутри трубки в положении 1 находится шарик массой m. Определить, как изменится угловая скорость трубки, если шарик перейдёт в положение 2.

 Теоретическая механика Д5.10 Теоретическая механика 2 150₽
11976




САМОСТОЯТЕЛЬНАЯ РАБОТА 1
Вариант 20.
Расчёт разветвлённой электрической цепи постоянного тока
Для данной электрической цепи определить с использованием законов Ома и Кирхгофа
1. Токи в ветвях
2. Мощность, развиваемую источником энергии, и мощность потребителей
3. Составить баланс мощности

Последняя цифра номера студенческого билета U, В R1, Ом R2, Ом R2, Ом R4, Ом R5, Ом
0 110 10 12 17 15 19
Электротехника 20 Разветвлённая электрическая цепь постоянного тока 150₽
12074




САМОСТОЯТЕЛЬНАЯ РАБОТА 1
Вариант 61.
Расчёт разветвлённой электрической цепи постоянного тока
Для данной электрической цепи определить с использованием законов Ома и Кирхгофа
1. Токи в ветвях
2. Мощность, развиваемую источником энергии, и мощность потребителей
3. Составить баланс мощности

Последняя цифра номера студенческого билета U, В R1, Ом R2, Ом R2, Ом R4, Ом R5, Ом
1 36 10 7 5 5 9
Электротехника 61 Разветвлённая электрическая цепь постоянного тока 150₽
16020

Тонкая проволока согнута в виде правильного n угольника, рамка несёт заряд Q, её сторона равна L. В центре рамки расположен точечный заряд q, потенциальная энергия которого в поле рамки равна W. Определить параметр, обозначенный в таблице для Вашего варианта знаком «?».

Вариант n, м Q, нКл L, м q нКл W, нДж
3 5 200 ? 500 1,2
Электроника 2-2-3 ЗабГУ. Физика. 2011 год 150₽
17906

Вычислить несобственный интеграл, используя вычеты: $$\int\limits_{0}^{+\infty} \frac{\cos{3x}}{x^4+1}dx$$

 Теория функций комплексного переменного 150₽
10304




Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии.
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 2, выполнить следующее:
1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений не следует.
2. Определить токи в ветвях методом контурных токов.
3. Определить режимы работы активных элементов и составить баланс мощностей.
Значения ЭДС источников и сопротивлений приемников приведены в табл. 2.

Предпоследняя цифра учебного шифра студента E1, В E2, В R1, Ом R2, Ом R3, Ом R4, Ом R5, Ом R6, Ом
7 120 140 10 8 13 20 15 21
Электротехника 271 МИИТ. Общая электротехника и электроника. 2016 год 150₽
16802




По двум проводящим шинам, находящимся в горизонтальной плоскости, может скользить без трения проводящая перемычка длиной l = 8 см, расположенная перпендикулярно шинам (рис. 20). Внешнее магнитное поле направлено вертикально, его индукция B = 0,05 Тл. Какую силу и в каком направлении надо приложить к перемычке, чтобы она не скользила? Е = 36 В,R = 20 Ом, внутренним сопротивлением источника, сопротивлением шин и перемычки пренебречь.

 Электромагнетизм 150₽

Страницы