Если найти нужную задачу не удаётся, Вы можете оформить Заказ.
Как использовать поиск
| Номер | Условие задачи | Предмет | Задачник |
Цена |
||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 12930 |
Диск массой m, имеющий радиус R, начинает вращаться под действием силы F, приложенной по касательной к образующей диска, перпендикулярно ею радиусу; при этом момент сил трения, действующий на диск, равен М1. За время t, отсчитанное oт начала движения, диск совершает N оборотов. Определить параметр, обозначенный в таблице данных для Вашего варианта знаком «?».
|
Механика | 5-18 | ЗабГУ. Физика. 2011 год | 150₽ | |||||||||||||||||||||||
| 16738 |
На железнодорожной платформе у начала второго вагона покоящегося поезда стоял пассажир. Поезд тронулся с места и далее двигался равноускоренно. При этом оказалось, что третий вагон поезда проезжал мимо пассажира в течение времени τ. В течение какого времени будет проезжать мимо пассажира пятый вагон? Вагоны поезда пронумерованы по порядку с начала поезда и имеют одинаковую длину. Пассажир неподвижен. |
Кинематика | 150₽ | |||||||||||||||||||||||||
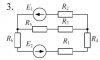
| 10340 |
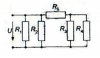
|
Электротехника | 233 | МИИТ. Общая электротехника и электроника. 2016 год | 150₽ | |||||||||||||||||||||||
| 13178 |
Средняя плотность планеты равна ρ, ее радиус – R, период обращения планеты вокруг своей оси – T. Найти вес тела массой m на экваторе планеты.
|
ФИЗИКА | 2-2-10 | ТГУ. Практические занятия по физике. 2019 год | 150₽ | |||||||||||||||||||||||
| 14388 |
Шлюпка массой 180 кг спущена на воду с борта судна, идущего со скоростью 3,0 м/с. Какое расстояние пройдёт шлюпка, пока её скорость не уменьшится в 10 раз? Насколько отстанет она от судна за это время? Сопротивления воды изменяется по закону $\vec{F}=-k_c\vec{v}$, где F - сила сопротивления, действующая на шлюпку, Н; kc = 90 Н∙с/м - коэффициент пропорциональности; v - скорость, м/с. |
Механика | 150₽ | |||||||||||||||||||||||||
| 6763 |
Найти все экстремали функционала $$J[y]=\int_{0}^{1}(y'^2-12xy)dx,$$ удовлетворяющие граничным условиям $y(0)=y(1)=0$. |
Вариационное исчисление | 150₽ | |||||||||||||||||||||||||
| 11706 |
Чему равен угол α между главными плоскостями поляризатора и анализатора, если интенсивность естественного света, прошедшего через анализатор и поляризатор, уменьшается в 4 раза? Коэффициент поглощения света в каждом поляроиде равен k = 10%. |
Оптика | 150₽ | |||||||||||||||||||||||||
| 14944 | Постоянный ток | 103 | Разветвлённая электрическая цепь постоянного тока | 150₽ | ||||||||||||||||||||||||
| 13194 |
Средняя плотность планеты равна ρ, ее радиус – R, период обращения планеты вокруг своей оси – T. Найти вес тела массой m на экваторе планеты.
|
ФИЗИКА | 2-2-18 | ТГУ. Практические занятия по физике. 2019 год | 150₽ | |||||||||||||||||||||||
| 10436 |
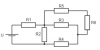
|
Электротехника | 214 | МИИТ. Общая электротехника и электроника. 2016 год | 150₽ | |||||||||||||||||||||||
| 9230 |
Найти экстремали функционалов в изопериметрической задаче: |
Вариационное исчисление | 4.23 | Вариационное исчисление | 150₽ | |||||||||||||||||||||||
| 11722 |
Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям: $$J[y]=\int_{-1}^{0}(12xy-{y'}^2)dx; y(-1)=1,\ y(0)=0$$ |
Вариационное исчисление | 2.17 | Вариационное исчисление | 150₽ | |||||||||||||||||||||||
| 14166 |
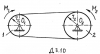
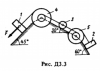
|
Теоретическая механика | D3.10 | МИИТ. Теоретическая механика. 2012 год | 150₽ | |||||||||||||||||||||||
| 16258 |
По обмотке тороида с ненамагниченным железным сердечником пустили ток силой 0,6 А. Витки провода диаметром 0,4 мм плотно прилегают друг к другу. Определить индуктивность тороида при данных условиях, а также энергию магнитного ноля в сердечнике, если площадь его сечения 4 см2, а диаметр средней линии 30 см. |
Электромагнетизм | 150₽ | |||||||||||||||||||||||||
| 12816 |
Автомобиль массой m, двигатель которого развивает тяговое усилие F, движется в подъём, угол наклона которого α. с ускорением a, коэффициент сопротивления движению K при этом на пути S совершается работа A. Используя таблицу данных согласно Вашему варианту, определить параметры, обозначенные в таблице данных знаком «?».
|
Механика | 3-13 | ЗабГУ. Физика. 2011 год | 150₽ | |||||||||||||||||||||||
| 11988 |
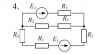
|
Электротехника | 24 | Разветвлённая электрическая цепь постоянного тока | 150₽ | |||||||||||||||||||||||
| 17898 |
Вычислить несобственный интеграл, используя вычеты: $$\int\limits_{-\infty}^{+\infty} \frac{x\sin {x}}{(x^2+4)(x^2+1)}dx$$ |
Теория функций комплексного переменного | 150₽ | |||||||||||||||||||||||||
| 12080 |
|
Электротехника | 64 | Разветвлённая электрическая цепь постоянного тока | 150₽ | |||||||||||||||||||||||
| 16026 |
Две одинаковые плоскопараллельные квадратные пластины, находящиеся в вакууме, образуют плоский конденсатор. Сторона пластины равна а, разность потенциалов между пластинами равна U. Вдоль оси симметрии конденсатора в него влетел со скоростью v электрон, который вылетает из конденсатора, отклонившись на расстояние h от оси симметрии и имея кинетическую энергию Т. Определить параметр, обозначенный в таблице для Вашего варианта знаком «?».
|
Электродинамика | 2-3-1 | ЗабГУ. Физика. 2011 год | 150₽ | |||||||||||||||||||||||
| 10618 |
Под действием силы F = f(s), зависящей от перемещения точки приложения силы, система приходит в движение из состояния покоя. При движении системы на шкив 5 действует постоянный момент сил сопротивлений, равный M5 = 0,8 Нм. Определить значение искомой величины в тот момент времени, когда перемещение точки приложения силы F равно S1 = 1 м. Искомая величина указана в столбце "Найти" таблицы, где обозначено: V1 - скорость груза 1. |
Теоретическая механика | 150₽ | |||||||||||||||||||||||||
| 12004 |
|
Электротехника | 32 | Разветвлённая электрическая цепь постоянного тока | 150₽ | |||||||||||||||||||||||
| 17906 |
Вычислить несобственный интеграл, используя вычеты: $$\int\limits_{0}^{+\infty} \frac{\cos{3x}}{x^4+1}dx$$ |
Теория функций комплексного переменного | 150₽ | |||||||||||||||||||||||||
| 16846 |
|
Электротехника | 150₽ | |||||||||||||||||||||||||
| 8866 |
Найти все экстремали функционала $J(y)$: $$J[y]=\int_{0}^{e}(y'^2-y^2+\frac{2ye^x}{x})e^{-2x}dx,$$ удовлетворяющие граничным условиям $y(1)=0; y(e)=e^{1+e}$ |
Вариационное исчисление | 2.1 | Вариационное исчисление | 150₽ | |||||||||||||||||||||||
| 12096 |
|
Электротехника | 72 | Разветвлённая электрическая цепь постоянного тока | 150₽ | |||||||||||||||||||||||
| 14524 |
Космический объект с массой покоя m0 движется со скоростью V имея импульс Р и кинетическую энергию Т. Собственная длина объекта в направлении движения l0, релятивистское изменение этой длины Δl. Определить параметры, обозначенные для Вашего варианта знаком “?"
|
Специальная теория относительности | 7-9 | ЗабГУ. Физика. 2011 год | 150₽ | |||||||||||||||||||||||
| 14688 |
Материальная точка массой m = 50 кг из состояния покоя движется по гладкой горизонтальной направляющей под действием силы F = 50 Н, вектор которой образует постоянный угол α = 60° с направляющей. Определить путь, пройденный точкой за время t = 2 с. |
Теоретическая механика | Д2.12 | Теоретическая механика 2 | 150₽ | |||||||||||||||||||||||
| 12026 |
|
Электротехника | 40 | Разветвлённая электрическая цепь постоянного тока | 150₽ | |||||||||||||||||||||||
| 17914 |
Вычислить несобственный интеграл, используя вычеты: $$\int\limits_{-\infty}^{+\infty} \frac{x\sin{2x}}{(x^2-2x+5)^2}dx$$ |
Теория функций комплексного переменного | 150₽ | |||||||||||||||||||||||||
| 6194 |
В процессе политропного сжатия воздуха G = 62∙103 кг/с, в одноступенчатом поршневом компрессоре отводится теплота в количестве Q = 1350 Дж/с. При сжатии от начального абсолютного давления p1 = 0,1∙106 Па температура воздуха возрастает от T1 = 288 К до T2 = 383 К. Определить показатель политропы процесса сжатия, конечное давление, удельную работу сжатия и техническую работу на получение сжатого воздуха, Дж/кг. Какова теоретически потребная мощность привода компрессора, кВт. |
Теплотехника | 150₽ | |||||||||||||||||||||||||
| 8888 |
Найти все экстремали функционала J(y), удовлетворяющие указанным граничным условиям: |
Вариационное исчисление | 2.2 | Вариационное исчисление | 150₽ | |||||||||||||||||||||||
| 12112 |
|
Электротехника | 80 | Разветвлённая электрическая цепь постоянного тока | 150₽ | |||||||||||||||||||||||
| 16058 |
|
Механика | 150₽ | |||||||||||||||||||||||||
| 14540 |
Космический объект с массой покоя m0 движется со скоростью V имея импульс Р и кинетическую энергию Т. Собственная длина объекта в направлении движения l0, релятивистское изменение этой длины Δl. Определить параметры, обозначенные для Вашего варианта знаком “?"
|
Специальная теория относительности | 7-17 | ЗабГУ. Физика. 2011 год | 150₽ | |||||||||||||||||||||||
| 10262 |
|
Электротехника | 222 | МИИТ. Общая электротехника и электроника. 2016 год | 150₽ | |||||||||||||||||||||||
| 13414 |
В сосуде объемом V при температуре T находится смесь двух идеальных газов с массами m1 и m2. Найти давление смеси p, молярную массу смеси M и число молекул в N сосуде.
|
ФИЗИКА | 4-1-6 | ТГУ. Практические занятия по физике. 2019 год | 150₽ | |||||||||||||||||||||||
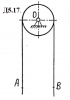
| 18173 |
Автомобиль преодолевает подъём с углом наклона α. Коэффициент трения колёс о дорогу равен f. Определить тормозной путь автомобиля, если его скорость в момент отключения двигателя и включения тормозного привода была равна v0. Колёса автомобиля считать полностью заторможенными. |
Кинематика | 150₽ | |||||||||||||||||||||||||
| 13494 |
Один моль идеального газа совершает процесс, в котором давление газа P убывает с увеличением его объема V по заданному закону P(V). Найти максимальную температуру газа в этом процессе.
|
ФИЗИКА | 4-3-6 | ТГУ. Практические занятия по физике. 2019 год | 150₽ | |||||||||||||||||||||||
| 11950 |
|
Электротехника | 07 | Разветвлённая электрическая цепь постоянного тока | 150₽ | |||||||||||||||||||||||
| 8806 |
Найти все экстремали функционала $J(y)$, |
Вариационное исчисление | 1.3 | Вариационное исчисление | 150₽ | |||||||||||||||||||||||
| 12048 |
|
Электротехника | 48 | Разветвлённая электрическая цепь постоянного тока | 150₽ | |||||||||||||||||||||||
| 14058 |
|
Теоретическая механика | Д5.17 | Теоретическая механика | 150₽ | |||||||||||||||||||||||
| 12132 |
|
Электротехника | 88 | Разветвлённая электрическая цепь постоянного тока | 150₽ | |||||||||||||||||||||||
| 18056 |
Разложить функцию $f(x)$ в ряд Фурье в указанном интервале. Выписать полученный ряд и три первых члена разложения отдельно. Построить графики функции $f(x)$ и её приближения: $$f(x)=x-3 \ в \ интервале \ (-\pi;\pi)$$ |
Ряды | 150₽ | |||||||||||||||||||||||||
| 14154 | Теоретическая механика | Д7.10 | Теоретическая механика 2 | 150₽ | ||||||||||||||||||||||||
| 14556 |
Космический объект с массой покоя m0 движется со скоростью V имея импульс Р и кинетическую энергию Т. Собственная длина объекта в направлении движения l0, релятивистское изменение этой длины Δl. Определить параметры, обозначенные для Вашего варианта знаком “?"
|
Специальная теория относительности | 7-25 | ЗабГУ. Физика. 2011 год | 150₽ | |||||||||||||||||||||||
| 13430 |
В сосуде объемом V при температуре T находится смесь двух идеальных газов с массами m1 и m2. Найти давление смеси p, молярную массу смеси M и число молекул в N сосуде.
|
ФИЗИКА | 4-1-14 | ТГУ. Практические занятия по физике. 2019 год | 150₽ | |||||||||||||||||||||||
| 13510 |
Один моль идеального газа совершает процесс, в котором давление газа P убывает с увеличением его объема V по заданному закону P(V). Найти максимальную температуру газа в этом процессе.
|
ФИЗИКА | 4-3-14 | ТГУ. Практические занятия по физике. 2019 год | 150₽ | |||||||||||||||||||||||
| 12716 |
Материальная точка движется по закону: $$\vec{r}=A\cdot t^m\cdot \vec{i}+B\cdot t^n \cdot \vec{j}+C\cdot t^l\cdot \vec{k}$$ Определить скорость и ускорение в момент времени $t_2$. перемещение точки в промежуток времени от $t_1$ до $t_2$, среднее значение скорости точки за этот же промежуток времени.
|
Механика | 1-15 | ЗабГУ. Физика. 2011 год | 150₽ | |||||||||||||||||||||||
| 4260 |
Две плоскопараллельные тонкие пластины заряжены, поверхностные плотности электрических зарядов на них равны соответственно σ1 и σ2 В поле, образованное этими пластинами, внесли слой диэлектрика с относительной диэлектрической проницаемостью ε толщиной d1 и слой металла толщиной d2. Расстояние между пластинами равно d = d1 + d2. Найти напряженность и потенциал электростатического поля:
|
Электростатика | 150₽ |