Если найти нужную задачу не удаётся, Вы можете оформить Заказ.
Как использовать поиск
| Номер | Условие задачи | Предмет | Задачник |
Цена |
|||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16460 | Электромагнетизм | 150₽ | |||||||||||||||||||||||||||||||||||||||||||||||
| 14544 |
Космический объект с массой покоя m0 движется со скоростью V имея импульс Р и кинетическую энергию Т. Собственная длина объекта в направлении движения l0, релятивистское изменение этой длины Δl. Определить параметры, обозначенные для Вашего варианта знаком “?"
|
Специальная теория относительности | 7-19 | ЗабГУ. Физика. 2011 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 13418 |
В сосуде объемом V при температуре T находится смесь двух идеальных газов с массами m1 и m2. Найти давление смеси p, молярную массу смеси M и число молекул в N сосуде.
|
ФИЗИКА | 4-1-8 | ТГУ. Практические занятия по физике. 2019 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 13498 |
Один моль идеального газа совершает процесс, в котором давление газа P убывает с увеличением его объема V по заданному закону P(V). Найти максимальную температуру газа в этом процессе.
|
ФИЗИКА | 4-3-8 | ТГУ. Практические занятия по физике. 2019 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 9920 |
Два контура в виде равностороннего треугольника и окружности радиусом 20 см расположены в двух взаимно перпендикулярных плоскостях. Центр окружности совпадает с одной из вершин треугольника. Сторона треугольника равна 20 см. В контурах протекают равные по величине токи силой 5 А. Определить (в мкТл) значение магнитной индукции в точке, совпадающей с центром окружности. |
Электромагнетизм | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 13192 |
Средняя плотность планеты равна ρ, ее радиус – R, период обращения планеты вокруг своей оси – T. Найти вес тела массой m на экваторе планеты.
|
ФИЗИКА | 2-2-17 | ТГУ. Практические занятия по физике. 2019 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
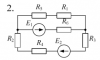
| 10434 |
|
Электротехника | 204 | МИИТ. Общая электротехника и электроника. 2016 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 6781 |
С помощью функции Вейерштрасса исследовать на экстремум функционал $$V[y]=\int_{1}^{e}[x^2{y'}^2+x]dx, y(1)=1,\ y(e)=2$$ |
Вариационное исчисление | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 10514 |
|
Электротехника | 297 | МИИТ. Общая электротехника и электроника. 2016 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 11720 |
Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям: $$J[y]=\int_0^1({y'}^2-y^2+4y\cos x)dx; y(0)=0,\ y(1)=0$$ |
Вариационное исчисление | 2.16 | Вариационное исчисление | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
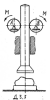
| 14164 |
D3.7. Фрикционный молот состоит из двух роликов и падающей ударной части. Масса каждого ролика равна m. найти ускорение падающей ударной части, массы m1 при её движении вверх, если к роликам приложены равные моменты М. Ролики считать однородными дисками. Скольжение между падающей частью и роликами отсутствует. |
Сопротивление материалов | D3.8 | МИИТ. Теоретическая механика. 2012 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 9004 |
ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ДЕЙСТВИЯ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ |
Теоретическая механика | C1.7. | МИИТ. Теоретическая механика. 2014 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 14246 |
Квадратная рамка со стороной 17,3 см шарнирно закреплена в серединах двух противоположных сторон. Две другие стороны параллельны длинному прямому проводу, удаленному от центра рамки на 5 см. Эти стороны равноудалены от провода. Какой механический вращательный момент действует на рамку, если ток по проводу 10 А, а по рамке – 1 А? |
Электромагнетизм | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 13520 |
Один моль идеального газа совершает процесс, в котором давление газа P убывает с увеличением его объема V по заданному закону P(V). Найти максимальную температуру газа в этом процессе.
|
ФИЗИКА | 4-3-19 | ТГУ. Практические занятия по физике. 2019 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 17864 |
Вычислить интеграл $$\oint\limits_{|z|=2} \frac{z^3 dz}{z^4-1}$$ |
Теория функций комплексного переменного | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 10450 |
|
Электротехника | 284 | МИИТ. Общая электротехника и электроника. 2016 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 4784 |
В начальный момент времени t1 = 0 поезд имеет скорость v1 и проходит пункт A, координата которого x1. Второй поезд через t2 секунд проходит со скоростью v2 пункт B, координата которого x2. Числовые значения координат, скоростей, ускорения а, характер движения поездов и направления движения приведены в таблице.
|
Механика | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 12894 |
Диск массой m, имеющий радиус R, начинает вращаться под действием силы F, приложенной по касательной к образующей диска, перпендикулярно ею радиусу; при этом момент сил трения, действующий на диск, равен М1. За время t, отсчитанное oт начала движения, диск совершает N оборотов. Определить параметр, обозначенный в таблице данных для Вашего варианта знаком «?».
|
Механика | 5-1 | ЗабГУ. Физика. 2011 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 11736 |
Найти все экстремали функционала $J(y)$: $$J[y]=\int_{1}^{e}(x^3 {y'}^2-xy^2+\frac{2y}{x})dx,$$ удовлетворяющие граничным условиям $y(1)=0;\ y(e)=1/e^2$. |
Вариационное исчисление | 2.27 | Вариационное исчисление | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 13536 |
Один моль идеального газа переходит из начального состояния 1 в конечное состояние 3 в результате двух процессов 1-2 и 2-3. Значения давления и объема газа в состояниях 1 и 3 равны соответственно P1, V1 и P3, V3. Найти работу, совершенную газом, количество теплоты Q, полученное газом и приращение внутренней энергии газа ΔU в процессе перехода из начального состояния 1 в конечное состояние 3.
|
ФИЗИКА | 5-1-7 | ТГУ. Практические занятия по физике. 2019 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 17872 |
Вычислить интеграл $$\oint\limits_{ |z|=\sqrt{3}} \frac{\sin{\pi z}\ dz}{z^2-z} $$ |
Теория функций комплексного переменного | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 9180 |
Найти экстремали функционалов: с дифференциальными связями: |
Вариационное исчисление | 4.15 | Вариационное исчисление | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 10466 |
|
Электротехника | 265 | МИИТ. Общая электротехника и электроника. 2016 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 11668 |
Найти все экстремали функционала $J(y)$: $$J[y]=\int_1^e({y'}^2+2y^2+8x^2ye^{x^2})dx,$$ удовлетворяющие граничным условиям $y(0)=1;\ y(1)=e$. |
Вариационное исчисление | 1.21 | Вариационное исчисление | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 12912 |
Диск массой m, имеющий радиус R, начинает вращаться под действием силы F, приложенной по касательной к образующей диска, перпендикулярно ею радиусу; при этом момент сил трения, действующий на диск, равен М1. За время t, отсчитанное oт начала движения, диск совершает N оборотов. Определить параметр, обозначенный в таблице данных для Вашего варианта знаком «?».
|
Механика | 5-9 | ЗабГУ. Физика. 2011 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 11752 |
Определить основные параметры рабочего тела в переходных точках идеального цикла поршневого двигателя внутреннего сгорания со смешанным подводом теплоты, степень сжатия, термический КПД и полезную работу. Заданы характеристики цикла λ = 1,8 и ρ = 1,4. В начальной точке цикла p1 = 0,1 МПа и t1 = 67° С. Температура в конце адиабатного процесса сжатия рабочего тела равна 600° С. Рабочее тело — 1 кг сухого воздуха. Изобразить цикл в pv и Ts-координатах.
|
Теплотехника | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 12256 |
Установка Юнга имеет следующие характеристики: расстояние между щелями d = 2 мм, расстояние L = 3 м. Щель S1 покрывают стеклянной пластинкой толщиной h = 0,01 мм, при этом интерференционные полосы смещаются на x = 7,8 мм. Найдите показатель преломления n стекла. Построить график распределения интенсивности света I. |
Оптика | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 10320 |
|
Электротехника | 262 | МИИТ. Общая электротехника и электроника. 2016 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 15072 |
По тонкой нити, изогнутой по дуге окружности радиусом R равномерно распределён заряд Q. На точечный заряд q, находящийся в центре дуги, составляющей 1/4 часть полной окружности, действует сила F. Определить параметр, обозначенный в таблице для Вашего варианта знаком «?».
|
Электростатика | 2-1-1 | ЗабГУ. Физика. 2011 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 13160 |
Средняя плотность планеты равна ρ, ее радиус – R, период обращения планеты вокруг своей оси – T. Найти вес тела массой m на экваторе планеты.
|
ФИЗИКА | 2-2-1 | ТГУ. Практические занятия по физике. 2019 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 13552 |
Один моль идеального газа переходит из начального состояния 1 в конечное состояние 3 в результате двух процессов 1-2 и 2-3. Значения давления и объема газа в состояниях 1 и 3 равны соответственно P1, V1 и P3, V3. Найти работу, совершенную газом, количество теплоты Q, полученное газом и приращение внутренней энергии газа ΔU в процессе перехода из начального состояния 1 в конечное состояние 3.
|
ФИЗИКА | 5-1-15 | ТГУ. Практические занятия по физике. 2019 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 17880 |
Вычислить интеграл $$\oint\limits_{ |z+1+i|=2} \frac{z^2 e^z}{z+1} dz $$ |
Теория функций комплексного переменного | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 10482 |
|
Электротехника | 246 | МИИТ. Общая электротехника и электроника. 2016 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 10562 |
|
Электротехника | 230 | МИИТ. Общая электротехника и электроника. 2016 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 12928 |
Диск массой m, имеющий радиус R, начинает вращаться под действием силы F, приложенной по касательной к образующей диска, перпендикулярно ею радиусу; при этом момент сил трения, действующий на диск, равен М1. За время t, отсчитанное oт начала движения, диск совершает N оборотов. Определить параметр, обозначенный в таблице данных для Вашего варианта знаком «?».
|
Механика | 5-17 | ЗабГУ. Физика. 2011 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 10338 |
|
Электротехника | 223 | МИИТ. Общая электротехника и электроника. 2016 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 13176 |
Средняя плотность планеты равна ρ, ее радиус – R, период обращения планеты вокруг своей оси – T. Найти вес тела массой m на экваторе планеты.
|
ФИЗИКА | 2-2-9 | ТГУ. Практические занятия по физике. 2019 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 11616 |
Найти все экстремали функционала $J(y)$, удовлетворяющие указанным граничным условиям: $$J[y]=\int_{\pi/6}^{\pi/4}({y'}^2-y^2+\frac{2y}{\sqrt{\sin^5 x\cos x}})dx;$$ $$y(\pi/6)=\frac{2}{\sqrt[4]{3}}; y(\pi/4)=\frac{2\sqrt{2}}{3}$$ |
Вариационное исчисление | 2.13 | Вариационное исчисление | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 10498 |
|
Электротехника | 217 | МИИТ. Общая электротехника и электроника. 2016 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 12944 |
Диск массой m, имеющий радиус R, начинает вращаться под действием силы F, приложенной по касательной к образующей диска, перпендикулярно ею радиусу; при этом момент сил трения, действующий на диск, равен М1. За время t, отсчитанное oт начала движения, диск совершает N оборотов. Определить параметр, обозначенный в таблице данных для Вашего варианта знаком «?».
|
Механика | 5-25 | ЗабГУ. Физика. 2011 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
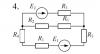
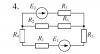
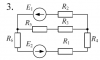
| 12130 |
|
Электротехника | 87 | Разветвлённая электрическая цепь постоянного тока | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
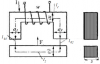
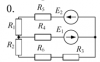
| 16474 |
|
Электродинамика | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||
| 14554 |
Космический объект с массой покоя m0 движется со скоростью V имея импульс Р и кинетическую энергию Т. Собственная длина объекта в направлении движения l0, релятивистское изменение этой длины Δl. Определить параметры, обозначенные для Вашего варианта знаком “?"
|
Специальная теория относительности | 7-24 | ЗабГУ. Физика. 2011 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 13428 |
В сосуде объемом V при температуре T находится смесь двух идеальных газов с массами m1 и m2. Найти давление смеси p, молярную массу смеси M и число молекул в N сосуде.
|
ФИЗИКА | 4-1-13 | ТГУ. Практические занятия по физике. 2019 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 13508 |
Один моль идеального газа совершает процесс, в котором давление газа P убывает с увеличением его объема V по заданному закону P(V). Найти максимальную температуру газа в этом процессе.
|
ФИЗИКА | 4-3-13 | ТГУ. Практические занятия по физике. 2019 год | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 14720 |
|
Теоретическая механика | Д5.5 | Теоретическая механика 2 | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 16788 |
Две взаимно перпендикулярные хорды окружности AB и CD пересекаются в точке M. Известно, что AD = 6, BC = 8 и центр окружности отстоит от точки M на расстоянии 1. |
Геометрия | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||
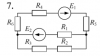
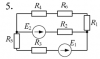
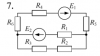
| 11964 |
|
Электротехника | 14 | Разветвлённая электрическая цепь постоянного тока | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||
| 16829 |
Докажите, что следующие множества равномощны: [3;7) и [3;7] |
Математическая логика | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||||
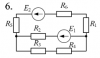
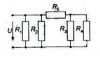
| 12062 |
|
Электротехника | 55 | Разветвлённая электрическая цепь постоянного тока | 150₽ | ||||||||||||||||||||||||||||||||||||||||||||