|
12972 |
Стержень массой m1 и длиной l1 может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В покоящийся стержень попала пуля массой m2, летевшая горизонтально со скоростью v перпендикулярно оси вращения стержня, от которой точка попадания пули находилась на расстоянии l2. После удара пули, имеющего неупругий характер, стержень отклонился на угол α. Определить параметр, обозначенный в таблице данных для Вашего варианта знаком «?».
| Номер варианта |
m1, кг |
l1, м |
m2, кг |
l2, м |
v, м/с |
α, град |
| 15 |
5 |
1,0 |
? |
0,8 |
700 |
41,0 |
|
Механика |
6-15 |
ЗабГУ. Физика. 2011 год |
250₽ |
|
|
13138 |
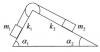
Два тела с массами m1 и m2 связаны невесомой нитью перекинутой через невесомый блок (Рис. 1). Наклонные плоскости, по которым скользят грузы, составляют с горизонтом углы α1 и α2 соответственно, а коэффициенты трения между грузами и плоскостями равны k1 и k2 соответственно. Трением в блоке можно пренебречь. В какую сторону движутся грузы - влево или вправо? Найти ускорение a грузов и силу натяжения T нити. Ускорение свободного падения g = 9,81 м/с2.
| № варианта |
m1, m2, α1, α2, k1, k2 |
| 10 |
m1 = 3 кг, m2 = 2 кг, α1 = 75°, α2 = 80°, k1 = 0,1, k2 = 0,1 |
|
ФИЗИКА |
2-1-10 |
ТГУ. Практические занятия по физике. 2019 год |
250₽ |
|
|
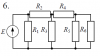
10078 |
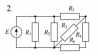
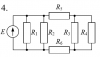
Расчет разветвленной линейной электрической цепи постоянного тока с одним источником электрической энергии
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 1, определить:
1. Токи в ветвях.
2. Мощность, развиваемую источником энергии и мощность потребителей. Проверить выполнение баланса мощностей.
Значения сопротивлений резисторов и ЭДС источника приведены в табл. 1
| Предпоследняя цифра учебного шифра студента |
E, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 0 |
150 |
17 |
6 |
9 |
18 |
7 |
16 |
|
Электротехника |
102 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
13226 |
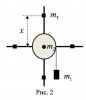
На однородный цилиндрический блок массой m2 и радиусом R намотана невесомая нить, к свободному концу которой прикреплен груз массой m1. К блоку крестообразно прикреплены четыре одинаковых невесомых стержня, на которых закреплены одинаковые грузы массой m3 на расстоянии x от оси вращения (Рис. 2). Грузы m3 можно считать материальными точками. Трением в блоке можно пренебречь. Найти зависимость ускорения a груза m1 от расстояния x. Построить график этой зависимости в интервале изменения x от R до 3R. Ускорение свободного падения g = 9,81 м/с2.
| № варианта |
R, m1, m2, m3 |
| 14 |
R = 0,3 м, m1 = 5 кг, m2 = 3 кг, m3 = 2 кг |
|
ФИЗИКА |
2-3-14 |
ТГУ. Практические занятия по физике. 2019 год |
250₽ |
|
|
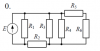
10160 |
Расчет разветвленной линейной электрической цепи постоянного тока с одним источником электрической энергии
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 1, определить:
1. Токи в ветвях.
2. Мощность, развиваемую источником энергии и мощность потребителей. Проверить выполнение баланса мощностей.
Значения сопротивлений резисторов и ЭДС источника приведены в табл. 1
| Предпоследняя цифра учебного шифра студента |
E, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 0 |
150 |
17 |
6 |
9 |
18 |
7 |
16 |
|
Электротехника |
105 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
13310 |
Груз массой m подвешен на невесомой нерастяжимой нити в поле силы тяжести. Нить с грузом отклонили от вертикали на угол α и отпустили. Найти зависимость от угла α силы натяжения нити T в момент прохождения грузом положения равновесия. Построить график этой зависимости в интервале изменения угла α от 0 до 180°. Найти максимальную силу натяжения T. Ускорение свободного падения g = 9,81 м/с2.
| № варианта |
m |
| 15 |
m = 20 кг |
|
ФИЗИКА |
3-2-15 |
ТГУ. Практические занятия по физике. 2019 год |
250₽ |
|
|
10240 |
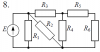
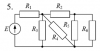
Расчет разветвленной линейной электрической цепи постоянного тока с одним источником электрической энергии
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 1, определить:
1. Токи в ветвях.
2. Мощность, развиваемую источником энергии и мощность потребителей. Проверить выполнение баланса мощностей.
Значения сопротивлений резисторов и ЭДС источника приведены в табл. 1
| Предпоследняя цифра учебного шифра студента |
E, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 9 |
140 |
12 |
11 |
10 |
9 |
16 |
15 |
|
Электротехника |
198 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
13392 |
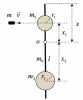
Тонкий однородный стержень массой m0 = 1 кг и длиной l = 4 м может вращаться в вертикальной плоскости вокруг горизонтальной оси O в поле силы тяжести (Рис. 3). Расстояние от верхнего конца стержня до оси вращения x = 1 м. На стержне жестко закреплены два однородных шара массами m1 = 1 кг и m2 = 3 кг и радиусами r1 = 10 см и r2 = 20 см. В равновесии первый шар находится над осью вращения, второй – под ней. Расстояния от центров шаров до оси вращения – x1 и x2 соответственно. В центр одного из шаров попадает пуля массой m = 30 г, летящая горизонтально со скоростью v = 500 м/с и застревает в нем. Масса пули много меньше массы шаров. Найти максимальный угол α, на который отклонится стержень с шарами после попадания пули. Пулю считать материальной точкой. Ускорение свободного падения g = 9,81 м/с2.
| № вариант |
шар, в который попадает пуля, x1, x2 |
| 15 |
верхний, x1 = 0,6 м, x2 = 1,0 м |
|
ФИЗИКА |
3-4-15 |
ТГУ. Практические занятия по физике. 2019 год |
250₽ |
|
|
8106 |
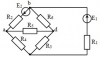
ЗАДАНИЕ № 1 «РАСЧЕТ ЦЕПИ ПОСТОЯННОГО ТОКА»
1.1. Для заданной согласно своему варианту электрической схемы составить систему уравнений по законам Кирхгофа, достаточную для определения токов ветвей. Полученную систему уравнений не решать.
1.2. Рассчитать токи во всех ветвях заданной электрической схемы методом контурных токов. Правильность расчетов проверить составлением баланса мощностей.
1.3. Примечания:
1) Первая цифра в трехзначном номере варианта, заданного преподавателем (как правило, три последние цифры в зачетной книжке студента), соответствует порядковому номеру строки в таблице 1.1, вторая цифра – порядковому номеру строки в таблице 1.2, третья цифра – номеру схемы на рис. 1.1.
2) Баланс мощностей должен сойтись с погрешностью менее 1%.
Таблица № 1.1
| № п/п |
E1, В |
E2, B |
| 4 |
19 |
16 |
Таблица № 1.2
| № п/п |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 5 |
6 |
7 |
10 |
5 |
3 |
2 |
|
Электротехника |
|
|
250₽ |
|
|
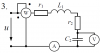
10628 |
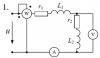
Расчет неразветвленной линейной цепи переменного тока.
Напряжение на зажимах цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 3, изменяется по закону $u=U_m \cdot \sin{\omega t}$. Амплитудное значение напряжения Um, значения активных сопротивлений r1 и r2, индуктивностей катушек L1 и L2, емкостей конденсаторов C1 и C2 приведены в табл. 3.
Частота питающего напряжения f = 50 Гц.
Необходимо:
1. Определить показания приборов, указанных на схеме рис. 3.
2. Построить векторную диаграмму токов и напряжений.
3. Определить закон изменения тока в цепи.
4. Определить закон изменения напряжения между точками, к которым подключен вольтметр.
5. Определить активную, реактивную и полную мощности источника, активную, реактивную и полную мощности приемников. Составить и оценить баланс мощностей. Рассчитать коэффициент мощности.
6. Определить характер (индуктивность, емкость) и параметры элемента, который должен быть включен в электрическую цепь для того, чтобы в ней имел место резонанс напряжений.
| Предпоследняя цифра учебного шифра студента |
Um, В |
r1, Ом |
r2, Ом |
L1, Гн |
L2, Гн |
C1, мкФ |
C2, мкФ |
| 4 |
200 |
3 |
4 |
0,04 |
0,03 |
250 |
300 |
|
Электротехника |
341 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
10708 |
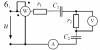
Расчет неразветвленной линейной цепи переменного тока.
Напряжение на зажимах цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 3, изменяется по закону $u=U_m \cdot \sin{\omega t}$. Амплитудное значение напряжения Um, значения активных сопротивлений r1 и r2, индуктивностей катушек L1 и L2, емкостей конденсаторов C1 и C2 приведены в табл. 3.
Частота питающего напряжения f = 50 Гц.
Необходимо:
1. Определить показания приборов, указанных на схеме рис. 3.
2. Построить векторную диаграмму токов и напряжений.
3. Определить закон изменения тока в цепи.
4. Определить закон изменения напряжения между точками, к которым подключен вольтметр.
5. Определить активную, реактивную и полную мощности источника, активную, реактивную и полную мощности приемников. Составить и оценить баланс мощностей. Рассчитать коэффициент мощности.
6. Определить характер (индуктивность, емкость) и параметры элемента, который должен быть включен в электрическую цепь для того, чтобы в ней имел место резонанс напряжений.
| Предпоследняя цифра учебного шифра студента |
Um, В |
r1, Ом |
r2, Ом |
L1, Гн |
L2, Гн |
C1, мкФ |
C2, мкФ |
| 1 |
180 |
4 |
16 |
0,02 |
0,03 |
300 |
250 |
|
Электротехника |
316 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
10790 |
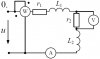
Расчет неразветвленной линейной цепи переменного тока.
Напряжение на зажимах цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 3, изменяется по закону $u=U_m \cdot \sin{\omega t}$. Амплитудное значение напряжения Um, значения активных сопротивлений r1 и r2, индуктивностей катушек L1 и L2, емкостей конденсаторов C1 и C2 приведены в табл. 3.
Частота питающего напряжения f = 50 Гц.
Необходимо:
1. Определить показания приборов, указанных на схеме рис. 3.
2. Построить векторную диаграмму токов и напряжений.
3. Определить закон изменения тока в цепи.
4. Определить закон изменения напряжения между точками, к которым подключен вольтметр.
5. Определить активную, реактивную и полную мощности источника, активную, реактивную и полную мощности приемников. Составить и оценить баланс мощностей. Рассчитать коэффициент мощности.
6. Определить характер (индуктивность, емкость) и параметры элемента, который должен быть включен в электрическую цепь для того, чтобы в ней имел место резонанс напряжений.
| Предпоследняя цифра учебного шифра студента |
Um, В |
r1, Ом |
r2, Ом |
L1, Гн |
L2, Гн |
C1, мкФ |
C2, мкФ |
| 1 |
180 |
4 |
16 |
0,02 |
0,03 |
300 |
250 |
|
Электротехника |
310 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
12844 |
С наклонной плоскости h, составляющей угол α с горизонтом, соскальзывает с начальной скоростью, равной нулю, шайба массой m1 после схода с наклонной плоскости ударяющаяся абсолютно упруго о неподвижную шайбу массой m2, которая после удара проходит по горизонтальной поверхности путь S. При движении обеих шайб коэффициент трения одинаков и равен К. Определить параметр, обозначенный в таблице данных для Вашего варианта знаком «?».
| Номер варианта |
h, м |
α, град |
m1, кг |
m2, кг |
k |
S, м |
| 2 |
8 |
? |
0,5 |
0,25 |
0,2 |
25,6 |
|
Механика |
4-2 |
ЗабГУ. Физика. 2011 год |
250₽ |
|
|
10094 |
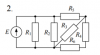
Расчет разветвленной линейной электрической цепи постоянного тока с одним источником электрической энергии
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 1, определить:
1. Токи в ветвях.
2. Мощность, развиваемую источником энергии и мощность потребителей. Проверить выполнение баланса мощностей.
Значения сопротивлений резисторов и ЭДС источника приведены в табл. 1
| Предпоследняя цифра учебного шифра студента |
E, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 8 |
130 |
16 |
9 |
13 |
14 |
11 |
7 |
|
Электротехника |
182 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
10176 |
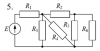
Расчет разветвленной линейной электрической цепи постоянного тока с одним источником электрической энергии
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 1, определить:
1. Токи в ветвях.
2. Мощность, развиваемую источником энергии и мощность потребителей. Проверить выполнение баланса мощностей.
Значения сопротивлений резисторов и ЭДС источника приведены в табл. 1
| Предпоследняя цифра учебного шифра студента |
E, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 8 |
130 |
16 |
9 |
13 |
14 |
11 |
7 |
|
Электротехника |
185 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
10256 |
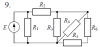
Расчет разветвленной линейной электрической цепи постоянного тока с одним источником электрической энергии
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 1, определить:
1. Токи в ветвях.
2. Мощность, развиваемую источником энергии и мощность потребителей. Проверить выполнение баланса мощностей.
Значения сопротивлений резисторов и ЭДС источника приведены в табл. 1
| Предпоследняя цифра учебного шифра студента |
E, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 7 |
120 |
7 |
6 |
14 |
9 |
15 |
10 |
|
Электротехника |
179 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
10724 |
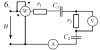
Расчет неразветвленной линейной цепи переменного тока.
Напряжение на зажимах цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 3, изменяется по закону $u=U_m \cdot \sin{\omega t}$. Амплитудное значение напряжения Um, значения активных сопротивлений r1 и r2, индуктивностей катушек L1 и L2, емкостей конденсаторов C1 и C2 приведены в табл. 3.
Частота питающего напряжения f = 50 Гц.
Необходимо:
1. Определить показания приборов, указанных на схеме рис. 3.
2. Построить векторную диаграмму токов и напряжений.
3. Определить закон изменения тока в цепи.
4. Определить закон изменения напряжения между точками, к которым подключен вольтметр.
5. Определить активную, реактивную и полную мощности источника, активную, реактивную и полную мощности приемников. Составить и оценить баланс мощностей. Рассчитать коэффициент мощности.
6. Определить характер (индуктивность, емкость) и параметры элемента, который должен быть включен в электрическую цепь для того, чтобы в ней имел место резонанс напряжений.
| Предпоследняя цифра учебного шифра студента |
Um, В |
r1, Ом |
r2, Ом |
L1, Гн |
L2, Гн |
C1, мкФ |
C2, мкФ |
| 9 |
320 |
7 |
5 |
0,03 |
0,04 |
500 |
200 |
|
Электротехника |
396 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
10806 |
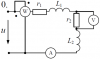
Расчет неразветвленной линейной цепи переменного тока.
Напряжение на зажимах цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 3, изменяется по закону $u=U_m \cdot \sin{\omega t}$. Амплитудное значение напряжения Um, значения активных сопротивлений r1 и r2, индуктивностей катушек L1 и L2, емкостей конденсаторов C1 и C2 приведены в табл. 3.
Частота питающего напряжения f = 50 Гц.
Необходимо:
1. Определить показания приборов, указанных на схеме рис. 3.
2. Построить векторную диаграмму токов и напряжений.
3. Определить закон изменения тока в цепи.
4. Определить закон изменения напряжения между точками, к которым подключен вольтметр.
5. Определить активную, реактивную и полную мощности источника, активную, реактивную и полную мощности приемников. Составить и оценить баланс мощностей. Рассчитать коэффициент мощности.
6. Определить характер (индуктивность, емкость) и параметры элемента, который должен быть включен в электрическую цепь для того, чтобы в ней имел место резонанс напряжений.
| Предпоследняя цифра учебного шифра студента |
Um, В |
r1, Ом |
r2, Ом |
L1, Гн |
L2, Гн |
C1, мкФ |
C2, мкФ |
| 9 |
320 |
7 |
5 |
0,03 |
0,04 |
500 |
200 |
|
Электротехника |
390 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
12862 |
С наклонной плоскости h, составляющей угол α с горизонтом, соскальзывает с начальной скоростью, равной нулю, шайба массой m1 после схода с наклонной плоскости ударяющаяся абсолютно упруго о неподвижную шайбу массой m2, которая после удара проходит по горизонтальной поверхности путь S. При движении обеих шайб коэффициент трения одинаков и равен К. Определить параметр, обозначенный в таблице данных для Вашего варианта знаком «?».
| Номер варианта |
h, м |
α, град |
m1, кг |
m2, кг |
k |
S, м |
| 10 |
1 |
60 |
0,8 |
? |
0,3 |
4,9 |
|
Механика |
4-10 |
ЗабГУ. Физика. 2011 год |
250₽ |
|
|
10112 |
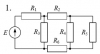
Расчет разветвленной линейной электрической цепи постоянного тока с одним источником электрической энергии
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 1, определить:
1. Токи в ветвях.
2. Мощность, развиваемую источником энергии и мощность потребителей. Проверить выполнение баланса мощностей.
Значения сопротивлений резисторов и ЭДС источника приведены в табл. 1
| Предпоследняя цифра учебного шифра студента |
E, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 6 |
110 |
7 |
8 |
12 |
14 |
13 |
8 |
|
Электротехника |
161 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
10192 |
Расчет разветвленной линейной электрической цепи постоянного тока с одним источником электрической энергии
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 1, определить:
1. Токи в ветвях.
2. Мощность, развиваемую источником энергии и мощность потребителей. Проверить выполнение баланса мощностей.
Значения сопротивлений резисторов и ЭДС источника приведены в табл. 1
| Предпоследняя цифра учебного шифра студента |
E, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 6 |
110 |
7 |
8 |
12 |
14 |
13 |
8 |
|
Электротехника |
166 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
10272 |
Расчет разветвленной линейной электрической цепи постоянного тока с одним источником электрической энергии
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 1, определить:
1. Токи в ветвях.
2. Мощность, развиваемую источником энергии и мощность потребителей. Проверить выполнение баланса мощностей.
Значения сопротивлений резисторов и ЭДС источника приведены в табл. 1
| Предпоследняя цифра учебного шифра студента |
E, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 4 |
90 |
13 |
14 |
16 |
8 |
10 |
15 |
|
Электротехника |
140 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
18064 |
Невесомый блок укреплён на вершине двух наклонных плоскостей, составляющих с горизонтом углы α1 и α2. Грузы массами m1 и m2 соединены невесомой и нерастяжимой нитью, перекинутой через блок. На грузы действует сила натяжения нити T. Коэффициент трения груза массой m1 о поверхность равен μ1, груза m2 равен μ2. Сила давления на ось блока Fd. Определить величины, указанные в таблице знаком вопроса.
| Номер варианта |
m1, кг |
m2, кг |
α1, град |
α2, град |
μ1 |
μ2 |
T, Н |
Fd, Н |
a, м/с2 |
| - |
249 |
1,0 |
30 |
45 |
- |
0,1 |
- |
? |
14 |
|
Механика |
|
|
250₽ |
|
|
10660 |
Расчет неразветвленной линейной цепи переменного тока.
Напряжение на зажимах цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 3, изменяется по закону $u=U_m \cdot \sin{\omega t}$. Амплитудное значение напряжения Um, значения активных сопротивлений r1 и r2, индуктивностей катушек L1 и L2, емкостей конденсаторов C1 и C2 приведены в табл. 3.
Частота питающего напряжения f = 50 Гц.
Необходимо:
1. Определить показания приборов, указанных на схеме рис. 3.
2. Построить векторную диаграмму токов и напряжений.
3. Определить закон изменения тока в цепи.
4. Определить закон изменения напряжения между точками, к которым подключен вольтметр.
5. Определить активную, реактивную и полную мощности источника, активную, реактивную и полную мощности приемников. Составить и оценить баланс мощностей. Рассчитать коэффициент мощности.
6. Определить характер (индуктивность, емкость) и параметры элемента, который должен быть включен в электрическую цепь для того, чтобы в ней имел место резонанс напряжений.
| Предпоследняя цифра учебного шифра студента |
Um, В |
r1, Ом |
r2, Ом |
L1, Гн |
L2, Гн |
C1, мкФ |
C2, мкФ |
| 7 |
160 |
6 |
12 |
0,01 |
0,01 |
300 |
200 |
|
Электротехника |
373 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
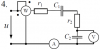
10740 |
Расчет неразветвленной линейной цепи переменного тока.
Напряжение на зажимах цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 3, изменяется по закону $u=U_m \cdot \sin{\omega t}$. Амплитудное значение напряжения Um, значения активных сопротивлений r1 и r2, индуктивностей катушек L1 и L2, емкостей конденсаторов C1 и C2 приведены в табл. 3.
Частота питающего напряжения f = 50 Гц.
Необходимо:
1. Определить показания приборов, указанных на схеме рис. 3.
2. Построить векторную диаграмму токов и напряжений.
3. Определить закон изменения тока в цепи.
4. Определить закон изменения напряжения между точками, к которым подключен вольтметр.
5. Определить активную, реактивную и полную мощности источника, активную, реактивную и полную мощности приемников. Составить и оценить баланс мощностей. Рассчитать коэффициент мощности.
6. Определить характер (индуктивность, емкость) и параметры элемента, который должен быть включен в электрическую цепь для того, чтобы в ней имел место резонанс напряжений.
| Предпоследняя цифра учебного шифра студента |
Um, В |
r1, Ом |
r2, Ом |
L1, Гн |
L2, Гн |
C1, мкФ |
C2, мкФ |
| 7 |
160 |
6 |
12 |
0,01 |
0,01 |
300 |
200 |
|
Электротехника |
377 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
12878 |
С наклонной плоскости h, составляющей угол α с горизонтом, соскальзывает с начальной скоростью, равной нулю, шайба массой m1 после схода с наклонной плоскости ударяющаяся абсолютно упруго о неподвижную шайбу массой m2, которая после удара проходит по горизонтальной поверхности путь S. При движении обеих шайб коэффициент трения одинаков и равен К. Определить параметр, обозначенный в таблице данных для Вашего варианта знаком «?».
| Номер варианта |
h, м |
α, град |
m1, кг |
m2, кг |
k |
S, м |
| 18 |
1,2 |
45 |
0,6 |
0,3 |
0,1 |
? |
|
Механика |
4-18 |
ЗабГУ. Физика. 2011 год |
250₽ |
|
|
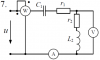
10128 |
Расчет разветвленной линейной электрической цепи постоянного тока с одним источником электрической энергии
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 1, определить:
1. Токи в ветвях.
2. Мощность, развиваемую источником энергии и мощность потребителей. Проверить выполнение баланса мощностей.
Значения сопротивлений резисторов и ЭДС источника приведены в табл. 1
| Предпоследняя цифра учебного шифра студента |
E, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 4 |
90 |
13 |
14 |
16 |
8 |
10 |
15 |
|
Электротехника |
143 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
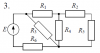
10208 |
Расчет разветвленной линейной электрической цепи постоянного тока с одним источником электрической энергии
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 1, определить:
1. Токи в ветвях.
2. Мощность, развиваемую источником энергии и мощность потребителей. Проверить выполнение баланса мощностей.
Значения сопротивлений резисторов и ЭДС источника приведены в табл. 1
| Предпоследняя цифра учебного шифра студента |
E, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 3 |
80 |
9 |
8 |
14 |
13 |
12 |
12 |
|
Электротехника |
137 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
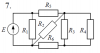
10676 |
Расчет неразветвленной линейной цепи переменного тока.
Напряжение на зажимах цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 3, изменяется по закону $u=U_m \cdot \sin{\omega t}$. Амплитудное значение напряжения Um, значения активных сопротивлений r1 и r2, индуктивностей катушек L1 и L2, емкостей конденсаторов C1 и C2 приведены в табл. 3.
Частота питающего напряжения f = 50 Гц.
Необходимо:
1. Определить показания приборов, указанных на схеме рис. 3.
2. Построить векторную диаграмму токов и напряжений.
3. Определить закон изменения тока в цепи.
4. Определить закон изменения напряжения между точками, к которым подключен вольтметр.
5. Определить активную, реактивную и полную мощности источника, активную, реактивную и полную мощности приемников. Составить и оценить баланс мощностей. Рассчитать коэффициент мощности.
6. Определить характер (индуктивность, емкость) и параметры элемента, который должен быть включен в электрическую цепь для того, чтобы в ней имел место резонанс напряжений.
| Предпоследняя цифра учебного шифра студента |
Um, В |
r1, Ом |
r2, Ом |
L1, Гн |
L2, Гн |
C1, мкФ |
C2, мкФ |
| 5 |
300 |
3 |
7 |
0,04 |
0,05 |
500 |
600 |
|
Электротехника |
354 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
10756 |
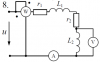
Расчет неразветвленной линейной цепи переменного тока.
Напряжение на зажимах цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 3, изменяется по закону $u=U_m \cdot \sin{\omega t}$. Амплитудное значение напряжения Um, значения активных сопротивлений r1 и r2, индуктивностей катушек L1 и L2, емкостей конденсаторов C1 и C2 приведены в табл. 3.
Частота питающего напряжения f = 50 Гц.
Необходимо:
1. Определить показания приборов, указанных на схеме рис. 3.
2. Построить векторную диаграмму токов и напряжений.
3. Определить закон изменения тока в цепи.
4. Определить закон изменения напряжения между точками, к которым подключен вольтметр.
5. Определить активную, реактивную и полную мощности источника, активную, реактивную и полную мощности приемников. Составить и оценить баланс мощностей. Рассчитать коэффициент мощности.
6. Определить характер (индуктивность, емкость) и параметры элемента, который должен быть включен в электрическую цепь для того, чтобы в ней имел место резонанс напряжений.
| Предпоследняя цифра учебного шифра студента |
Um, В |
r1, Ом |
r2, Ом |
L1, Гн |
L2, Гн |
C1, мкФ |
C2, мкФ |
| 5 |
300 |
3 |
7 |
0,04 |
0,05 |
500 |
600 |
|
Электротехника |
358 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
13210 |
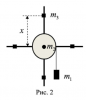
На однородный цилиндрический блок массой m2 и радиусом R намотана невесомая нить, к свободному концу которой прикреплен груз массой m1. К блоку крестообразно прикреплены четыре одинаковых невесомых стержня, на которых закреплены одинаковые грузы массой m3 на расстоянии x от оси вращения (Рис. 2). Грузы m3 можно считать материальными точками. Трением в блоке можно пренебречь. Найти зависимость ускорения a груза m1 от расстояния x. Построить график этой зависимости в интервале изменения x от R до 3R. Ускорение свободного падения g = 9,81 м/с2.
| № варианта |
R, m1, m2, m3 |
| 6 |
R = 0,2 м, m1 = 2 кг, m2 = 2 кг, m3 = 1 кг |
|
ФИЗИКА |
2-3-6 |
ТГУ. Практические занятия по физике. 2019 год |
250₽ |
|
|
10144 |
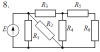
Расчет разветвленной линейной электрической цепи постоянного тока с одним источником электрической энергии
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 1, определить:
1. Токи в ветвях.
2. Мощность, развиваемую источником энергии и мощность потребителей. Проверить выполнение баланса мощностей.
Значения сопротивлений резисторов и ЭДС источника приведены в табл. 1
| Предпоследняя цифра учебного шифра студента |
E, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 2 |
70 |
13 |
10 |
10 |
11 |
15 |
17 |
|
Электротехника |
124 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
13294 |
Груз массой m подвешен на невесомой нерастяжимой нити в поле силы тяжести. Нить с грузом отклонили от вертикали на угол α и отпустили. Найти зависимость от угла α силы натяжения нити T в момент прохождения грузом положения равновесия. Построить график этой зависимости в интервале изменения угла α от 0 до 180°. Найти максимальную силу натяжения T. Ускорение свободного падения g = 9,81 м/с2.
|
ФИЗИКА |
3-2-7 |
ТГУ. Практические занятия по физике. 2019 год |
250₽ |
|
|
10224 |
Расчет разветвленной линейной электрической цепи постоянного тока с одним источником электрической энергии
Для электрической цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 1, определить:
1. Токи в ветвях.
2. Мощность, развиваемую источником энергии и мощность потребителей. Проверить выполнение баланса мощностей.
Значения сопротивлений резисторов и ЭДС источника приведены в табл. 1
| Предпоследняя цифра учебного шифра студента |
E, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
| 1 |
60 |
9 |
8 |
7 |
15 |
14 |
13 |
|
Электротехника |
118 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
13376 |
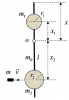
Тонкий однородный стержень массой m0 = 1 кг и длиной l = 4 м может вращаться в вертикальной плоскости вокруг горизонтальной оси O в поле силы тяжести (Рис. 3). Расстояние от верхнего конца стержня до оси вращения x = 1 м. На стержне жестко закреплены два однородных шара массами m1 = 1 кг и m2 = 3 кг и радиусами r1 = 10 см и r2 = 20 см. В равновесии первый шар находится над осью вращения, второй – под ней. Расстояния от центров шаров до оси вращения – x1 и x2 соответственно. В центр одного из шаров попадает пуля массой m = 30 г, летящая горизонтально со скоростью v = 500 м/с и застревает в нем. Масса пули много меньше массы шаров. Найти максимальный угол α, на который отклонится стержень с шарами после попадания пули. Пулю считать материальной точкой. Ускорение свободного падения g = 9,81 м/с2.
| № вариант |
шар, в который попадает пуля, x1, x2 |
| 7 |
нижний, x1 = 0,3 м, x2 = 0,9 м |
|
ФИЗИКА |
3-4-7 |
ТГУ. Практические занятия по физике. 2019 год |
250₽ |
|
|
10692 |
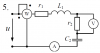
Расчет неразветвленной линейной цепи переменного тока.
Напряжение на зажимах цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 3, изменяется по закону $u=U_m \cdot \sin{\omega t}$. Амплитудное значение напряжения Um, значения активных сопротивлений r1 и r2, индуктивностей катушек L1 и L2, емкостей конденсаторов C1 и C2 приведены в табл. 3.
Частота питающего напряжения f = 50 Гц.
Необходимо:
1. Определить показания приборов, указанных на схеме рис. 3.
2. Построить векторную диаграмму токов и напряжений.
3. Определить закон изменения тока в цепи.
4. Определить закон изменения напряжения между точками, к которым подключен вольтметр.
5. Определить активную, реактивную и полную мощности источника, активную, реактивную и полную мощности приемников. Составить и оценить баланс мощностей. Рассчитать коэффициент мощности.
6. Определить характер (индуктивность, емкость) и параметры элемента, который должен быть включен в электрическую цепь для того, чтобы в ней имел место резонанс напряжений.
| Предпоследняя цифра учебного шифра студента |
Um, В |
r1, Ом |
r2, Ом |
L1, Гн |
L2, Гн |
C1, мкФ |
C2, мкФ |
| 3 |
460 |
4 |
6 |
0,02 |
0,02 |
250 |
800 |
|
Электротехника |
335 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
10774 |
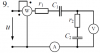
Расчет неразветвленной линейной цепи переменного тока.
Напряжение на зажимах цепи, вариант которой соответствует последней цифре учебного шифра студента и изображенной на рис. 3, изменяется по закону $u=U_m \cdot \sin{\omega t}$. Амплитудное значение напряжения Um, значения активных сопротивлений r1 и r2, индуктивностей катушек L1 и L2, емкостей конденсаторов C1 и C2 приведены в табл. 3.
Частота питающего напряжения f = 50 Гц.
Необходимо:
1. Определить показания приборов, указанных на схеме рис. 3.
2. Построить векторную диаграмму токов и напряжений.
3. Определить закон изменения тока в цепи.
4. Определить закон изменения напряжения между точками, к которым подключен вольтметр.
5. Определить активную, реактивную и полную мощности источника, активную, реактивную и полную мощности приемников. Составить и оценить баланс мощностей. Рассчитать коэффициент мощности.
6. Определить характер (индуктивность, емкость) и параметры элемента, который должен быть включен в электрическую цепь для того, чтобы в ней имел место резонанс напряжений.
| Предпоследняя цифра учебного шифра студента |
Um, В |
r1, Ом |
r2, Ом |
L1, Гн |
L2, Гн |
C1, мкФ |
C2, мкФ |
| 3 |
460 |
4 |
6 |
0,02 |
0,02 |
250 |
800 |
|
Электротехника |
339 |
МИИТ. Общая электротехника и электроника. 2016 год |
250₽ |
|
|
11096 |
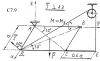
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ ПРОСТРАНСТВЕННОЙ КОНСТРУКЦИИ
Определить реакции связей пространственной конструкции, находящейся под действием сил F, P и пары сил с моментом М. Для всех вариантов принять F = 200 H, P = 300 H, M = 60 Нм, a = 1 м, схемы конструкций представлены на рисунке.
|
Теоретическая механика |
C7.9 |
Теоретическая механика 2 |
300₽ |
|
|
12334 |
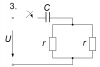
РАСЧЁТ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХ ПРИ ПОСТОЯННОЙ ЭДС ИСТОЧНИКА
Цепь, изображенная на рис. 1, подключается к источнику постоянного напряжения U 100 В. Значения напряжения источника, сопротивлений резисторов, величины индуктивностей и емкостей приведены в табл. 1.
| Предпоследняя цифра учебного шрифта студента |
r, Ом |
L, мГн |
C, мкФ |
| 5 |
15 |
- |
60 |
Необходимо:
1. Определить начальные значения токов и напряжений (до и сразу после коммутации).
2. Определить принужденные значения токов и напряжений.
3. Определить постоянную времени цепи.
4. Построить графики изменения во времени токов в ветвях и напряжений на участках цепи на основе начальных и принужденных значений для моментов времени r, 2ττ
Примечание к заданию: определять значения и строить графики только токи в ветви с индуктивностью (если в схеме индуктивность) или только напряжения на емкости (если в схеме емкость).
|
Электротехника |
153 |
СамГУПС Саратов. Общая электротехника и электроника. 2018 год |
300₽ |
|
|
11176 |
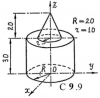
ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ЦЕНТРА ТЯЖЕСТИ ОДНОРОДНОГО ТЕЛА
Найти положение центра тяжести плоской фермы, пластинки и объемного тела. Ферма состоит из однородных стержней; пластинка имеет малую постоянную толщину. Схемы тел показаны на рис. C9.9. Размеры ферм даны в метрах, остальных тел - в сантиметрах.
|
Теоретическая механика |
C9.9 |
Теоретическая механика 2 |
300₽ |
|
|
12414 |

РАСЧЁТ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХ ПРИ ПОСТОЯННОЙ ЭДС ИСТОЧНИКА
Цепь, изображенная на рис. 1, подключается к источнику постоянного напряжения U 100 В. Значения напряжения источника, сопротивлений резисторов, величины индуктивностей и емкостей приведены в табл. 1.
| Предпоследняя цифра учебного шрифта студента |
r, Ом |
L, мГн |
C, мкФ |
| 0 |
50 |
30 |
- |
Необходимо:
1. Определить начальные значения токов и напряжений (до и сразу после коммутации).
2. Определить принужденные значения токов и напряжений.
3. Определить постоянную времени цепи.
4. Построить графики изменения во времени токов в ветвях и напряжений на участках цепи на основе начальных и принужденных значений для моментов времени r, 2ττ
Примечание к заданию: определять значения и строить графики только токи в ветви с индуктивностью (если в схеме индуктивность) или только напряжения на емкости (если в схеме емкость).
|
Электротехника |
107 |
СамГУПС Саратов. Общая электротехника и электроника. 2018 год |
300₽ |
|
|
8492 |
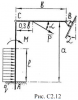
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ СОСТАВНОЙ ПЛОСКОЙ КОНСТРУКЦИИ
Определить реакции связей в точках А и В составной плоской конструкции, состоящей из двух твердых тел. Схемы конструкций приведены на рис. С2.12, исходные данные указаны в таблице 3.
| Номер варианта |
Р, кН |
М, кН м |
q, кН/м |
a, м |
b, м |
l, м |
α, град |
| С2.12 |
7 |
4.8 |
2 |
1.5 |
3.0 |
1.3 |
30° |
|
Теоретическая механика |
C2.12_1 |
Теоретическая механика |
300₽ |
|
|
10952 |
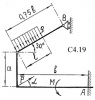
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ СОСТАВНОЙ ПЛОСКОЙ КОНСТРУКЦИИ
Определить реакции связей в точках А и В составной плоской конструкции, состоящей из двух твердых тел. Схемы конструкций приведены на рис. C4.19, исходные данные указаны в таблице 3.
| Номер варианта |
Р, кН |
М, кН м |
q, кН/м |
a, м |
b, м |
l, м |
α, град |
| C4.19 |
5 |
4 |
3 |
2.5 |
2.0 |
1.3 |
30° |
|
Теоретическая механика |
C4.19 |
Теоретическая механика 2 |
300₽ |
|
|
11032 |
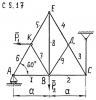
ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ ПЛОСКОЙ ФЕРМЫ
Определить усилия в стержнях плоской фермы рис. C5.17 соответственно способом разрезов Риттера и способом вырезания стержней с узлом фермы. Номера стержней и исходные данные указаны в табл. 4
| Номер варианта |
Номера стержней |
Номера стержней |
Р1, кН |
Р2, кН |
| C5.17 |
1, 7, 5 |
2, 3 |
130 |
150 |
|
Теоретическая механика |
C5.17 |
Теоретическая механика 2 |
300₽ |
|
|
11112 |
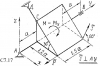
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ ПРОСТРАНСТВЕННОЙ КОНСТРУКЦИИ
Определить реакции связей пространственной конструкции, находящейся под действием сил F, P и пары сил с моментом М. Для всех вариантов принять F = 200 H, P = 300 H, M = 60 Нм, a = 1 м, схемы конструкций представлены на рисунке.
|
Теоретическая механика |
C7.17 |
Теоретическая механика 2 |
300₽ |
|
|
12350 |
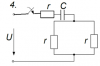
РАСЧЁТ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХ ПРИ ПОСТОЯННОЙ ЭДС ИСТОЧНИКА
Цепь, изображенная на рис. 1, подключается к источнику постоянного напряжения U 100 В. Значения напряжения источника, сопротивлений резисторов, величины индуктивностей и емкостей приведены в табл. 1.
| Предпоследняя цифра учебного шрифта студента |
r, Ом |
L, мГн |
C, мкФ |
| 1 |
15 |
- |
100 |
Необходимо:
1. Определить начальные значения токов и напряжений (до и сразу после коммутации).
2. Определить принужденные значения токов и напряжений.
3. Определить постоянную времени цепи.
4. Построить графики изменения во времени токов в ветвях и напряжений на участках цепи на основе начальных и принужденных значений для моментов времени r, 2ττ
Примечание к заданию: определять значения и строить графики только токи в ветви с индуктивностью (если в схеме индуктивность) или только напряжения на емкости (если в схеме емкость).
|
Электротехника |
114 |
СамГУПС Саратов. Общая электротехника и электроника. 2018 год |
300₽ |
|
|
11192 |
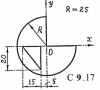
ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ЦЕНТРА ТЯЖЕСТИ ОДНОРОДНОГО ТЕЛА
Найти положение центра тяжести плоской фермы, пластинки и объемного тела. Ферма состоит из однородных стержней; пластинка имеет малую постоянную толщину. Схемы тел показаны на рис. C9.17. Размеры ферм даны в метрах, остальных тел - в сантиметрах.
|
Теоретическая механика |
C9.17 |
Теоретическая механика 2 |
300₽ |
|
|
12430 |
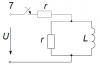
РАСЧЁТ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХ ПРИ ПОСТОЯННОЙ ЭДС ИСТОЧНИКА
Цепь, изображенная на рис. 1, подключается к источнику постоянного напряжения U 100 В. Значения напряжения источника, сопротивлений резисторов, величины индуктивностей и емкостей приведены в табл. 1.
| Предпоследняя цифра учебного шрифта студента |
r, Ом |
L, мГн |
C, мкФ |
| 8 |
20 |
80 |
- |
Необходимо:
1. Определить начальные значения токов и напряжений (до и сразу после коммутации).
2. Определить принужденные значения токов и напряжений.
3. Определить постоянную времени цепи.
4. Построить графики изменения во времени токов в ветвях и напряжений на участках цепи на основе начальных и принужденных значений для моментов времени r, 2ττ
Примечание к заданию: определять значения и строить графики только токи в ветви с индуктивностью (если в схеме индуктивность) или только напряжения на емкости (если в схеме емкость).
|
Электротехника |
187 |
СамГУПС Саратов. Общая электротехника и электроника. 2018 год |
300₽ |
|
|
18259 |

Шарик массы m движется из положения A внутри изогнутой трубки, расположенной в вертикальной плоскости. Шарик, пройдя путь l0, отделяется oт пружины. В точке B шарик, не меняя значения своей скорости, переходит на участок BC, где на него дополнительно действует переменная сила F, направление которой указано на рисунке. Пользуясь общими теоремами динамики точки, определить скорость шарика в положениях B и C. В задании принята следующие обозначения: vA - начальная скорость шарика, AB - длина участка, τ - время движения на участке BC, f - коэффициент трения скольжения шарика по стенке трубки, c - коэффициент жесткости пружины.
| № |
Рис. |
m |
vA |
f |
AB |
l0 |
c |
α |
β |
τ |
F(t) |
| 9 |
|
кг |
м/с |
|
м |
см |
Н/см |
град |
с |
Н |
| 6.1 |
0,5 |
4 |
0,1 |
0,3 |
5 |
1,5 |
45 |
- |
1 |
1,2cos 0,5t |
|
Механика |
|
|
300₽ |
|
|
5106 |

К валу электромотора, вращающемуся согласно уравнению $\varphi = \omega t$, прикреплен под прямым углом стержень ОА длиной l. Электромотор, установленный без креплений, совершает гармонические колебания по закону $x = b \cos \omega t$. Определить абсолютную скорость точки А стержня в момент времени $t_1 = \frac{\pi}{2\omega}$.
|
Теоретическая механика |
K7.10 |
Теоретическая механика 2 |
300₽ |
|










































